Giải Toán 10 trang 76 Tập 1 Cánh diều

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 76 Tập 1 trong Bài 2: Giải tam giác. Tính diện tích tam giác Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 76.

Giải Toán 10 trang 76 Tập 1 Cánh diều

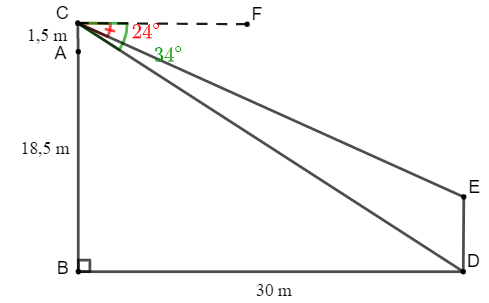
Luyện tập 2 trang 76 Toán lớp 10 Tập 1: Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34°, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

Giả sử toà nhà là AB, AB = 18,5 m; giác kế AC = 1,5 m; chiều cao của cái cây là DE; khoảng cách từ tòa nhà tới cây là BD = 30 m; góc tạo bởi phương quan sát gốc cây và phương nằm ngang là $\widehat{FCD}=34°$, góc tạo bởi phương quan sát ngọn cây và phương nằm ngang là $\widehat{FCE}=24°$. Ta cần tính DE. 

Hình vẽ mô phỏng: 

Ta có: BC = BA + AC = 18,5 + 1,5 = 20 (m). 

Tam giác BCD vuông tại B, áp dụng định lí Pythagore ta có: 

CD² = BC² + BD² = 20² + 30² = 1300 (m)$\Rightarrow CD=10\sqrt{13}$.

 Lại có: $\widehat{FCD}=\widehat{FCE}+\widehat{ECD}$

$\Rightarrow \widehat{ECD}=\widehat{FCD}-\widehat{FCE}=34°-24°=10°$

CF // BD $\Rightarrow \widehat{CDB}=\widehat{FCD}=34°$(so le trong)

$\Rightarrow \widehat{CDE}=90°-\widehat{CDB}=90°-34°=56°$

Tam giác CDE có $\widehat{ECD}+\widehat{CDE}+\widehat{CED}=180°$(định lí tổng ba góc trong tam giác)

$\Rightarrow \widehat{CED}=180°-\left(\widehat{ECD}+\widehat{CDE}\right)=180°-\left(10°+56°\right)=114°$.

Áp dụng định lí sin trong tam giác CDE ta có: $\frac{CD}{\sin \widehat{CED}}=\frac{DE}{\sin \widehat{ECD}}$

$\Rightarrow DE=\frac{CD.\sin \widehat{ECD}}{\sin \widehat{CED}}=\frac{10\sqrt{13}.\sin 10°}{\sin 114°}\approx 6,9$ (m)

Vậy chiều cao của cây khoảng 6,9 m.

Lời giải bài tập Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác Cánh diều hay khác:

• Giải Toán 10 trang 72 Tập 1
• Giải Toán 10 trang 73 Tập 1
• Giải Toán 10 trang 74 Tập 1
• Giải Toán 10 trang 75 Tập 1
• Giải Toán 10 trang 77 Tập 1