Giải Toán 10 trang 73 Tập 1 Cánh diều

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 73 Tập 1 trong Bài 2: Giải tam giác. Tính diện tích tam giác Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 73.

Giải Toán 10 trang 73 Tập 1 Cánh diều

Hoạt động 2 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, BC = a. Viết công thức tính cos A theo a, b, c.

Lời giải:

Áp dụng hệ quả của định lí côsin trong tam giác ABC ta có: 

$\cos A=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{c^2+b^2-a^2}{2bc}$

Vậy $\cos A=\frac{c^2+b^2-a^2}{2bc}$.

Hoạt động 3 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, $\widehat{B}=\alpha ,\widehat{C}=\beta$. Viết công thức tính AB và AC theo a, α, β.

Lời giải:

Tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ $\Rightarrow \widehat{A}=180°-\left(\widehat{B}+\widehat{C}\right)$

$\Rightarrow \widehat{A}=180°-\left(\alpha +\beta \right)$

⇒ sinA = sin(180° – (α + β)) = sin(α + β).

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}$

Suy ra: $AB=\frac{BC\sin C}{\sin A}=\frac{a.\sin \beta }{\sin \left(\alpha +\beta \right)}$ và $AC=\frac{BC\sin B}{\sin A}=\frac{a.\sin \alpha }{\sin \left(\alpha +\beta \right)}$.

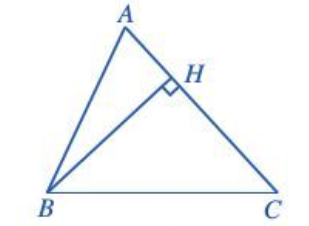
Hoạt động 4 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, BC = a. Kẻ đường cao BH.

a) Tính BH theo c và sin A. 

b) Tính diện tích S của tam giác ABC theo b, c, và sin A. 

Lời giải:

a) Xét các trường hợp:        

+ Với $\widehat{A}<90°$

Xét tam giác vuông AHB, ta có: BH = AB . sin A = c sin A. 

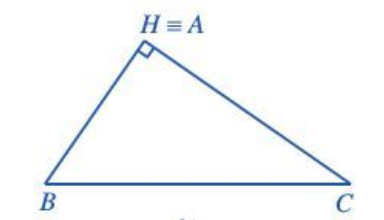
+ Với $\widehat{A}=90°$

Khi đó, BH = BA = c = c sin A. 

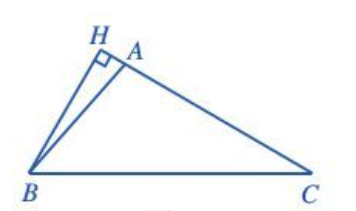
+ Với $\widehat{A}>90°$

Xét tam giác AHB vuông, ta có: $\widehat{BAH}=180°-\widehat{A}$.

Do đó BH = AB . sin(180° – $\widehat{A}$) = AB . sin A = c sin A. 

Như vậy, trong mọi trường hợp ta đều có BH = c sin A. 

b) Ta có: 

$S=\frac{1}{2}AC.BH=\frac{1}{2}bc\sin A$

Lời giải bài tập Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác Cánh diều hay khác:

• Giải Toán 10 trang 72 Tập 1
• Giải Toán 10 trang 74 Tập 1
• Giải Toán 10 trang 75 Tập 1
• Giải Toán 10 trang 76 Tập 1
• Giải Toán 10 trang 77 Tập 1