Hoạt động 1 trang 67 Toán lớp 10 Tập 2 Cánh diều

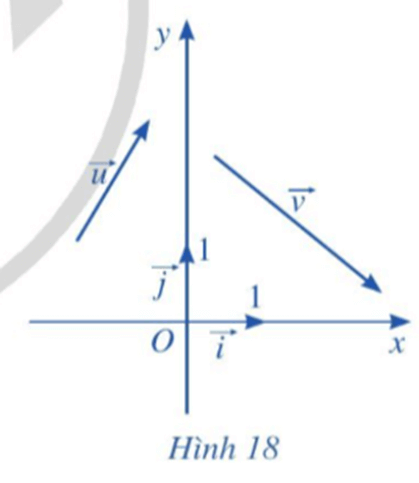
Trong mặt phẳng tọa độ Oxy (Hình 18), cho hai vectơ và .

Giải Toán lớp 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ

Hoạt động 1 trang 67 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy (Hình 18), cho hai vectơ $\vec{u} = (x_{1}; y_{1})$ và $\vec{v} = (x_{2}; y_{2})$ .

a) Biểu diễn các vectơ $\vec{u}, \vec{v}$ theo hai vectơ $\vec{i}$ và $\vec{j}$ .

b) Biểu diễn các vectơ $\vec{u} + \vec{v}, \vec{u} - \vec{v}$ , $k \vec{u}$ (k ∈ ℝ) theo hai vectơ $\vec{i}$ và $\vec{j}$ .

c) Tìm tọa độ các vectơ $\vec{u} + \vec{v}, \vec{u} - \vec{v}$ , $k \vec{u}$ (k ∈ ℝ).

Lời giải:

a) Do $\vec{u} = (x_{1}; y_{1})$ và $\vec{v} = (x_{2}; y_{2})$ nên $\vec{u} = x_{1} \vec{i} + y_{1} \vec{j}, \vec{v} = x_{2} \vec{i} + y_{2} \vec{j}$ .

b) Để biểu diễn vectơ $\vec{u} + \vec{v}$ theo hai vectơ $\vec{i}$ và $\vec{j}$ , ta làm như sau:

Do $\vec{u} = x_{1} \vec{i} + y_{1} \vec{j}, \vec{v} = x_{2} \vec{i} + y_{2} \vec{j}$ , vậy nên:

$\vec{u} + \vec{v} = (x_{1} \vec{i} + y_{1} \vec{j}) + (x_{2} \vec{i} + y_{2} \vec{j}) = (x_{1} \vec{i} + x_{2} \vec{i}) + (y_{1} \vec{j} + y_{2} \vec{j}) = (x_{1} + x_{2}) \vec{i} + (y_{1} + y_{2}) \vec{j}$

Tương tự, ta có:

$\vec{u} - \vec{v}$ $= (x_{1} \vec{i} + y_{1} \vec{j}) - (x_{2} \vec{i} + y_{2} \vec{j})$ $= (x_{1} \vec{i} - x_{2} \vec{i}) + (y_{1} \vec{j} - y_{2} \vec{j})$ $= (x_{1} - x_{2}) \vec{i} + (y_{1} - y_{2}) \vec{j}$ .

$k \vec{u} = k (x_{1} \vec{i} + y_{1} \vec{j}) = k x_{1} \vec{i} + k y_{1} \vec{j} = (k x_{1}) \vec{i} + (k y_{1}) \vec{j}$ (k ∈ ℝ).

c) Do $\vec{u} + \vec{v}$ $= (x_{1} + x_{2}) \vec{i} + (y_{1} + y_{2}) \vec{j}$ nên tọa độ vectơ $\vec{u} + \vec{v}$ là (x₁ + x₂; y₁ + y₂).

Do $\vec{u} - \vec{v}$ $= (x_{1} - x_{2}) \vec{i} + (y_{1} - y_{2}) \vec{j}$ nên tọa độ vectơ $\vec{u} - \vec{v}$ là (x₁ – x₂; y₁ – y₂).

Do $k \vec{u} = (k x_{1}) \vec{i} + (k y_{1}) \vec{j}$ nên tọa độ vectơ $k \vec{u}$ là (kx₁; ky₁) với (k ∈ ℝ).

Lời giải Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ hay, chi tiết khác:

Giải Toán lớp 10 Cánh diều

Hoạt động 1 trang 67 Toán lớp 10 Tập 2 Cánh diều

Giải Toán lớp 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: