Tam giác ABC có AB=3, AC=6, góc BAC=60 độ . Tính độ dài đường cao h kẻ từ đỉnh

Câu hỏi:

Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính độ dài đường cao h kẻ từ đỉnh A xuống cạnh BC của tam giác.

A. $h = 3 \sqrt{3}$

B. $h = \sqrt{3}$

C. $h = 3$

D. $h = \frac{3}{2}$

Trả lời:

Đáp án đúng là: C

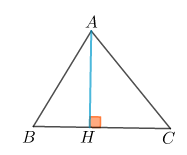
Áp dụng định lý hàm số cosin, ta có:

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C \cos A = 27 \Rightarrow B C = 3 \sqrt{3}$ (đơn vị độ dài).

Ta có: $S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} .3.6. \sin 60^{0} = \frac{9 \sqrt{3}}{2}$ (đơn vị diện tích).

Lại có $S_{Δ A B C} = \frac{1}{2} . B C . h_{a} \Rightarrow h_{a} = \frac{2 S}{B C} = 3$ (đơn vị độ dài).

Câu 1:

Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính diện tích tam giác ABC.

Câu 2:

Tam giác ABC có $A C = 4, \hat{B A C} = 30 °, \hat{A C B} = 75 °$ . Tính diện tích tam giác ABC.

Câu 3:

Tam giác ABC có a = 21, b = 17, c = 10 .Diện tích của tam giác ABC bằng:

Câu 4:

Tam giác ABC có $A C = 4, \hat{A C B} = 60 °$ . Tính độ dài đường cao h xuất phát từ đỉnh A của tam giác.

Câu 5:

Tam giác ABC có a = 21, b = 17, c = 10 . Gọi B’ là hình chiếu vuông góc của B trên cạnh AC. Tính BB’.

Câu 6:

Tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng $64 {cm}^{2}$ . Giá trị sinA bằng:

Câu 7:

Hình bình hành ABCD có $A B = a, B C = a \sqrt{2}$ và $\hat{B A D} = 45^{0}$ . Khi đó hình bình hành có diện tích bằng:

Giải Toán lớp 10 Cánh diều