Hình bình hành ABCD có AB=a, BC=a căn bậc hai 2 và góc BAD =45 độ. Khi đó hình
Câu hỏi:
Hình bình hành ABCD có và . Khi đó hình bình hành có diện tích bằng:
A.
B.
C.
D.
Trả lời:
Đáp án đúng là: C
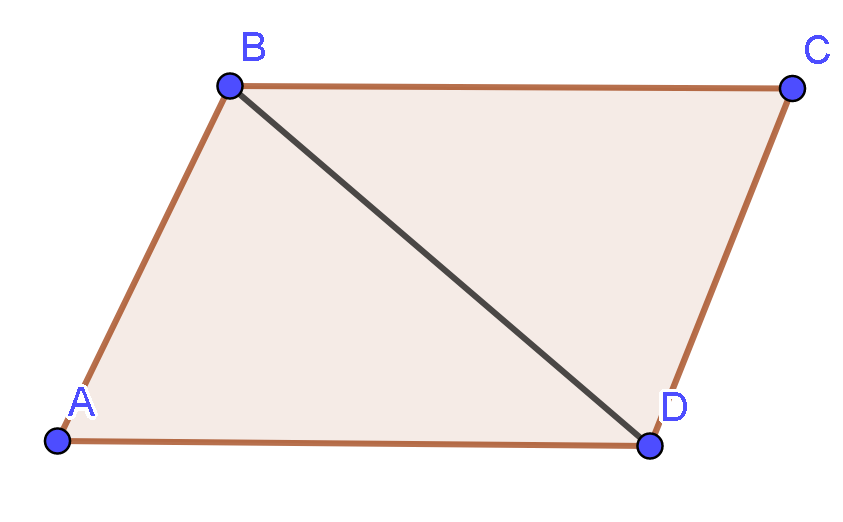
Diện tích tam giác ABD là: (đơn vị diện tích).(BC = AD = a)
Vậy diện tích hình bình hành ABCD là (đơn vị diện tích)

