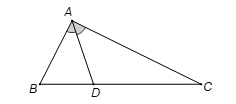
Tam giác ABC vuông tại A, có AB = c, AC = b. Gọi D là chân đường phân giác trong góc A. Tính AD theo b và c.
Câu hỏi:
Tam giác ABC vuông tại A, có AB = c, AC = b. Gọi D là chân đường phân giác trong góc A. Tính AD theo b và c.
A. AD = ;
Trả lời:
Đáp án đúng là: A