Từ hai vị trí A và B của một toà nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m
Câu hỏi:
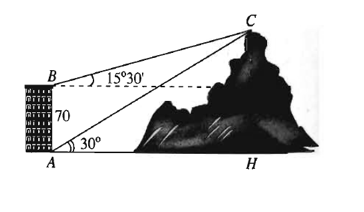
Từ hai vị trí A và B của một toà nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30’. Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
A. 135 m;
B. 234 m;
C. 165 m;
D. 195 m.
Trả lời:
Đáp án đúng là: A
Từ giả thiết, ta suy ra tam giác ABC có , và AB = 70.
Theo định lí tổng ba góc trong tam giác ABC có:
Theo định lí sin trong tam giác ABC, ta có hay .
Do đó
Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc 30° nên
Vậy ngọn núi cao khoảng 135 m.
