Tập nghiệm S của bất phương trình x^2 + x - 12 < 0 là:

Câu hỏi:

Tập nghiệm S của bất phương trình $x^{2}$ + x - 12 < 0 là:

A. $S = (- 4; 3);$

B. $S = (4; + \infty);$

C. $S = (3; + \infty);$

D. $S = \emptyset .$

Trả lời:

Đáp án đúng là: A

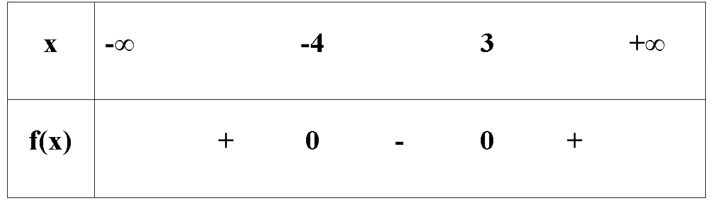
Tam thức bậc hai f(x) = $x^{2}$ + x - 12 có a = 1 > 0 và có hai nghiệm x = -4; x = 3. Ta có bảng xét dấu:

f(x) < 0 suy ra -4 < x < 3.

Câu 1:

Điểm nào sau đây thuộc đồ thị hàm số y = 4x + 1

Câu 2:

Cho hàm số y = f(x) = $|3 x|$ . Khẳng định nào sau đây là đúng?

Câu 3:

Tập xác định của hàm số y = $\frac{3 x - 1}{2 x - 2}$ là:

Câu 4:

Tập xác định của hàm số y = $\sqrt{x - 1}$ là:

Câu 5:

Tập nghiệm S của phương trình

\sqrt{2 x - 3} = x - 3

là:

Câu 6:

Phương trình $\sqrt{2 - x} + \frac{4}{\sqrt{2 - x} + 3} = 2$ có tất cả bao nhiêu nghiệm?

Câu 7:

Tổng các nghiệm của phương trình $(x - 2) \sqrt{2 x + 7} = x^{2} - 4$ bằng:

Câu 8:

Nghiệm của phương trình $\sqrt{3 x - 4} = \sqrt{4 - 3 x}$ là đáp án nào trong số các đáp án sau đây?

Giải Toán lớp 10 Cánh diều