Trong mặt phẳng tọa độ Oxy, cho vecto g = ( 2x;1 - 3y ) và vec h = ( x - y;3y - x ). Khi đó vec g = vec h khi và chỉ khi: A. x = 1/7 \\y = - 1/7; B. x = 1/3 \\y = 1/3;
Câu hỏi:
Trong mặt phẳng tọa độ Oxy, cho \[\vec g = \left( {2x;1 - 3y} \right)\] và \[\vec h = \left( {x - y;3y - x} \right)\]. Khi đó \(\vec g = \vec h\) khi và chỉ khi:
A. \(\left\{ \begin{array}{l}x = \frac{1}{7}\\y = - \frac{1}{7}\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = \frac{1}{3}\\y = \frac{1}{3}\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = - \frac{1}{7}\\y = \frac{1}{7}\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right.\).
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Ta có \(\vec g = \vec h\).
\( \Leftrightarrow \left\{ \begin{array}{l}2x = x - y\\1 - 3y = 3y - x\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x + y = 0\\x - 6y = - 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{1}{7}\\y = \frac{1}{7}\end{array} \right.\)
Vậy \(\left\{ \begin{array}{l}x = - \frac{1}{7}\\y = \frac{1}{7}\end{array} \right.\) thì \(\vec g = \vec h\).
Do đó ta chọn phương án C.
Xem thêm bài tập Toán 10 CD có lời giải hay khác:
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho hai điểm B(–1; 3) và C(5; 2). Tọa độ của \(\overrightarrow {BC} \) là:
Xem lời giải »
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho ba điểm E (2; – 3), F(4; 7), G(1; 5). Nếu \(\overrightarrow {EF} = \overrightarrow {GH} \) thì tọa độ điểm H là:
Xem lời giải »
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho \[\vec a = \left( {1;5} \right)\] và \(\vec b = \left( {3u + v;u - 2v} \right)\). Khi đó \(\vec a = \vec b\) khi và chỉ khi:
Xem lời giải »
Câu 5:
Cho điểm A(–2; 3) và \(\overrightarrow {AM} = 3\vec i - 2\vec j\).
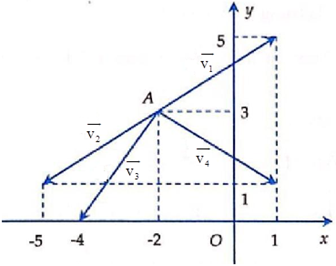
Vectơ nào trong hình là \(\overrightarrow {AM} \)?
Xem lời giải »