Bài 1 trang 32 Toán 10 Tập 1 Chân trời sáng tạo
Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0.
Giải Toán lớp 10 Bài 1: Bất phương trình bậc nhất hai ẩn
Bài 1 trang 32 Toán lớp 10 Tập 1: Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0.
a) (0 ; 0) có phải là một nghiệm của bất phương trình đã cho không ?
b) Chỉ ra ba cặp số (x ; y) là nghiệm của bất phương trình đã cho.
c) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng tọa độ Oxy.
Lời giải:
a) Với cặp (0 ; 0) ta có : 0 – 2.0 + 6 = 6 > 0 nên (0 ; 0) là nghiệm của bất phương trình đã cho.
Vậy (0 ; 0) là một nghiệm của bất phương trình x - 2y + 6 > 0.
b)
+ Lấy cặp số (1 ; 0) ta có 1 – 2.0 + 6 = 7 > 0 nên cặp số (1 ; 0) là một nghiệm của bất phương trình x - 2y + 6 > 0.
+ Lấy cặp số (0 ; 1) ta có 0 – 2.1 + 6 = 4 > 0 nên cặp số (0 ; 1) là một nghiệm của bất phương trình x - 2y + 6 > 0.
+ Lấy cặp số (-1 ; -1) ta có –1 – 2. (–1) + 6 = 7 > 0 nên cặp số (-1 ; -1) là một nghiệm của bất phương trình x - 2y + 6 > 0.
Vậy ta có ba cặp số (1 ; 0) ; (0 ; 1) ; (-1 ; -1) đều là nghiệm của bất phương trình x - 2y + 6 > 0.
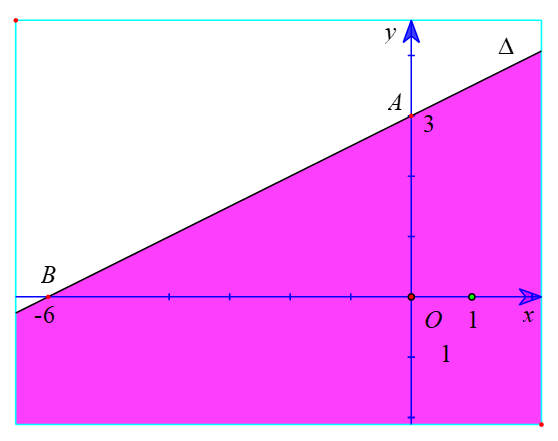
c) Vẽ đường thẳng ∆ : x – 2y + 6 = 0 đi qua hai điểm A(0; 3); B(-6; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và (0 ; 0) là một nghiệm của bất phương trình
x - 2y + 6 > 0.
Do đó, miền nghiệm của bất phương trình x - 2y + 6 > 0 là nửa mặt phẳng không kể bờ ∆, chứa điểm O (là miền được tô màu trong hình sau).
Lời giải bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác: