Bài 3 trang 10 Toán 10 Tập 2 Chân trời sáng tạo

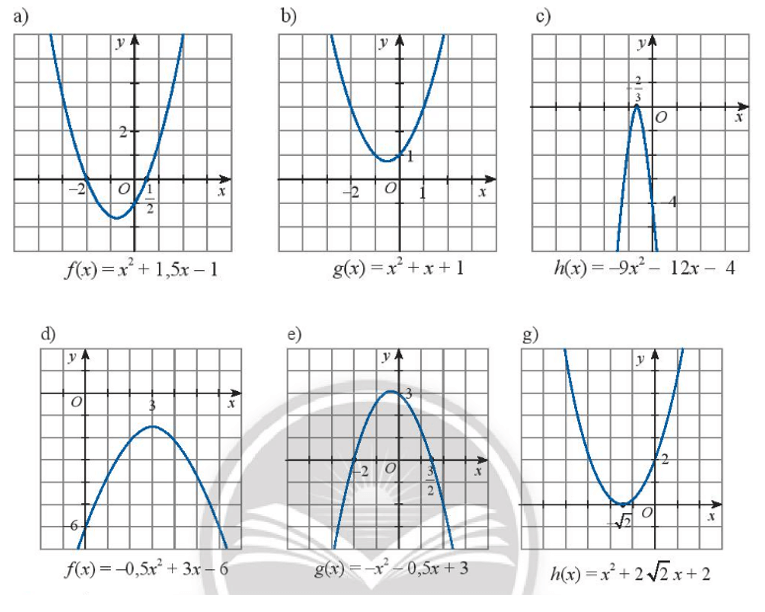
Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng.

Giải Toán lớp 10 Bài 1: Dấu của tam thức bậc hai

Bài 3 trang 10 Toán lớp 10 Tập 2: Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng.

Bài 3 trang 10 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán lớp 10

Lời giải:

a) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x₁ = - 2 và x₂ = $\frac{1}{2}$ . Do đó f(x) có hai nghiệm phân biệt x₁ = - 2, x₂ = $\frac{1}{2}$ và a = 1 > 0.

Với x thuộc khoảng (-∞; -2) và $(\frac{1}{2}; + \infty)$ thì đồ thị hàm số nằm phía trên trục hoành hay f(x) > 0 khi x thuộc khoảng (-∞; -2) và $(\frac{1}{2}; + \infty)$ .

Với x thuộc khoảng $(- 2; \frac{1}{2})$ thì đồ thị hàm số nằm dưới trục hoành hay f(x) < 0 khi x ∈ $(- 2; \frac{1}{2})$ .

Ta có bảng xét dấu f(x) như sau:

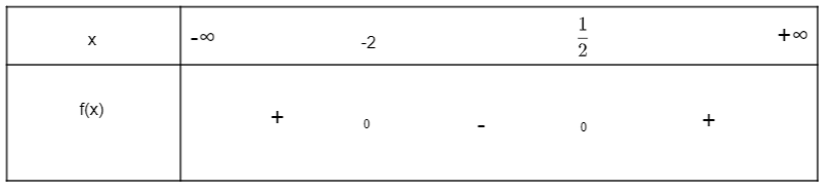
b) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số không cắt trục hoành. Do đó g(x) vô nghiệm và a = 1 > 0.

Hơn nữa toàn bộ đồ thị hàm số g(x) nằm phía trên trục hoành với mọi giá trị của x nên g(x) > 0 với mọi x.

Ta có bảng xét dấu f(x) như sau:

c) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số h(x) cắt trục hoành tại một điểm duy nhất có hoành độ x = $- \frac{2}{3}$ . Do đó h(x) có nghiệm duy nhất x = $- \frac{2}{3}$ và a = - 9 < 0.

Với x = $- \frac{2}{3}$ thì h(x) = 0;

Với x ≠ $- \frac{2}{3}$ thì đồ thị hàm số h(x) nằm hoàn toàn dưới trục hoành nên h(x) < 0 với x ≠ $- \frac{2}{3}$ .

Khi đó ta có bảng xét dấu:

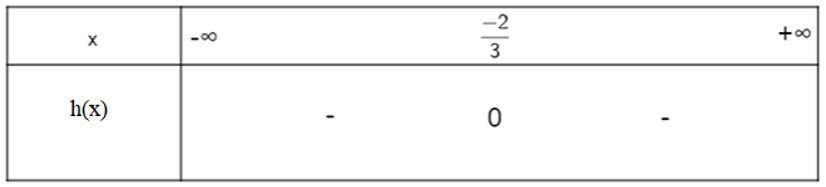
d) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số không cắt trục hoành. Do đó f(x) vô nghiệm và a = -0,5 < 0.

Hơn nữa toàn bộ đồ thị hàm số f(x) nằm phía dưới trục hoành với mọi giá trị của x nên f(x) < 0 với mọi x.

Ta có bảng xét dấu f(x) như sau:

e) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x₁ = - 2 và x₂ = $\frac{3}{2}$ . Do đó g(x) có hai nghiệm phân biệt x₁ = - 2, x₂ = $\frac{3}{2}$ và a = -1 < 0.

Với x thuộc khoảng (-∞; -2) và $(\frac{3}{2}; + \infty)$ thì đồ thị hàm số nằm phía dưới trục hoành hay g(x) < 0 khi x thuộc khoảng (-∞; -2) và $(\frac{3}{2}; + \infty)$ .

Với x thuộc khoảng $(- 2; \frac{3}{2})$ thì đồ thị hàm số nằm trên trục hoành hay g(x) > 0 khi x ∈ $(- 2; \frac{3}{2})$ .

Ta có bảng xét dấu g(x) như sau:

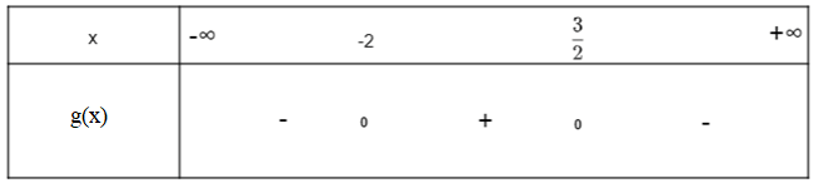
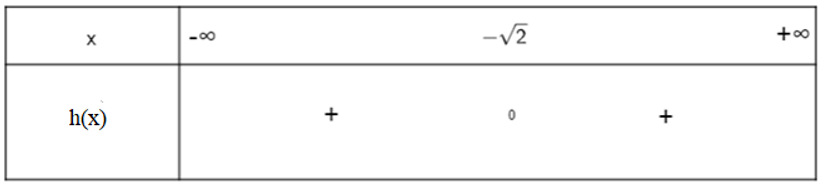
g) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số h(x) cắt trục hoành tại một điểm duy nhất có hoành độ x = $- \sqrt{2}$ . Do đó h(x) có nghiệm duy nhất x = $- \sqrt{2}$ và a = 1 > 0.

Với x = $- \sqrt{2}$ thì h(x) = 0;

Với x ≠ $- \sqrt{2}$ thì đồ thị hàm số h(x) nằm hoàn toàn phía trên trục hoành nên h(x) > 0 với x ≠ $- \frac{2}{3}$ .

Khi đó ta có bảng xét dấu:

Lời giải bài tập Toán 10 Bài 1: Dấu của tam thức bậc hai hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯