Bài 7 trang 10 Toán 10 Tập 2 Chân trời sáng tạo
Chứng minh rằng với mọi số thực m ta luôn có 9m + 2m > - 3.
Giải Toán lớp 10 Bài 1: Dấu của tam thức bậc hai
Bài 7 trang 10 Toán lớp 10 Tập 2: Chứng minh rằng với mọi số thực m ta luôn có 9m2 + 2m > - 3.
Lời giải:
Ta có: 9m2 + 2m > - 3
⇔ 9m2 + 2m + 3 > 0
Đặt f(m) = 9m2 + 2m + 3
Ta thấy f(m) là tam thức bậc hai với a = 9, b = 2 và c = 3.
Ta có: ∆ = 22 – 4.9.3 = 4 – 108 = -104 < 0. Do đó f(m) vô nghiệm và a = 9 > 0.
Khi đó ta có bảng xét dấu:
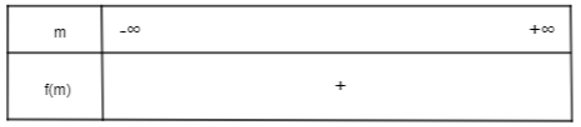
Từ bảng xét dấu ta thấy f(m) > 0 với mọi m
⇒ 9m2 + 2m + 3 > 0 với mọi m hay 9m2 + 2m > - 3 với mọi m.
Vậy 9m2 + 2m > - 3 với mọi m.
Lời giải bài tập Toán 10 Bài 1: Dấu của tam thức bậc hai hay, chi tiết khác:

