Bài 4 trang 10 Toán 10 Tập 2 Chân trời sáng tạo
Xét dấu của tam thức bậc hai sau đây:
Giải Toán lớp 10 Bài 1: Dấu của tam thức bậc hai
Bài 4 trang 10 Toán lớp 10 Tập 2: Xét dấu của tam thức bậc hai sau đây:
a) f(x) = 2x2 + 4x + 2;
b) f(x) = - 3x2 + 2x + 21;
c) f(x) = - 2x2 + x – 2;
d) f(x) = -4x(x + 3) – 9;
e) f(x) = (2x + 5)(x – 3).
Lời giải:
a) Tam thức bậc hai f(x) = 2x2 + 4x + 2 có ∆ = 42 – 4.2.2 = 16 – 16 = 0. Do đó f(x) có một nghiệm kép x1 = x2 = - 1 và a = 2 > 0.
Ta có bảng xét dấu sau:
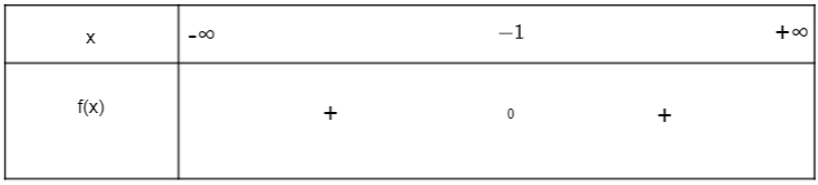
Vậy f(x) = 2x2 + 4x + 2 mang dấu dương khi x ≠ - 1.
b) Tam thức bậc hai f(x) = - 3x2 + 2x + 21 có ∆ = 22 – 4.(-3).21 = 256 > 0. Do đó f(x) có hai nghiệm phân biệt x1 = 3 và x2 = và a = -3 < 0.
Ta có bảng xét dấu:
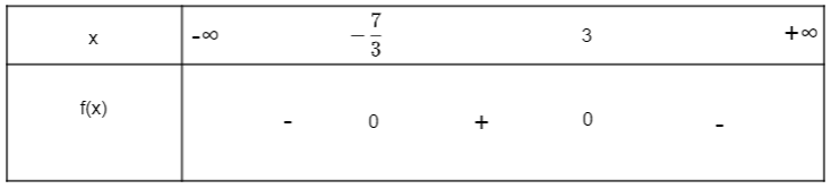
Vậy f(x) = - 3x2 + 2x + 21 dương khi x thuộc khoảng và f(x) = - 3x2 + 2x + 21 âm khi x thuộc hai khoảng và .
c) Tam thức bậc hai f(x) = - 2x2 + x – 2 có ∆ = 12 – 4.(-2).(-2) = 1 – 16 = -15 < 0. Do đó hàm số vô nghiệm và a = -2 < 0.
Ta có bảng xét dấu:

Vậy f(x) = - 2x2 + x – 2 âm với mọi giá trị thực của x.
d) Ta có f(x) = -4x(x + 3) – 9 = - 4x2 – 12x – 9.
Xét tam thức f(x) = - 4x2 – 12x – 9 có ∆ = (-12)2 – 4.(-4)(-9) = 144 – 144 = 0. Do đó f(x) có nghiệm kép x1 = x2 = và a = - 4 < 0.
Ta có bảng xét dấu:
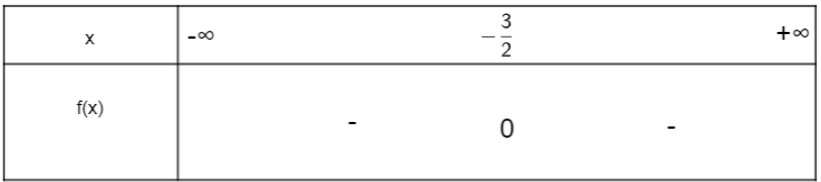
Vậy f(x) mang dấu âm khi x ≠ .
e) Ta có f(x) = (2x + 5)(x – 3) = 2x2 – 6x + 5x – 15 = 2x2 – x – 15.
Tam thức f(x) = 2x2 – x – 15 có ∆ = (-1)2 – 4.2.(-15) = 1 + 120 = 121 > 0. Do đó f(x) có hai nghiệm phân biệt x1 = 3 và x2 = và a = 2 > 0.
Ta có bảng xét dấu:
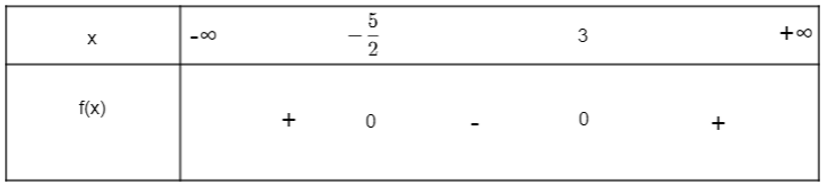
Vậy f(x) = (2x + 5)(x – 3) âm khi x thuộc khoảng và f(x) = (2x + 5)(x – 3) dương khi x thuộc hai khoảng và (3; +∞).
Lời giải bài tập Toán 10 Bài 1: Dấu của tam thức bậc hai hay, chi tiết khác:

