Cho A = {x ∈ ℝ | x + 2 ≥ 0}, B = {x ∈ ℝ | 5 – x ≥ 0}. Khi đó A \ B là: A. [–2; 5]; B. [–2; 6]; C. (5; +∞); D. (2; +∞).
Câu hỏi:
Cho A = {x ∈ ℝ | x + 2 ≥ 0}, B = {x ∈ ℝ | 5 – x ≥ 0}. Khi đó A \ B là:
A. [–2; 5];
B. [–2; 6];
C. (5; +∞);
D. (2; +∞).
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
⦁ Ta có x + 2 ≥ 0.
Û x ≥ –2.
Do đó tập A = [–2; +∞).
⦁ Ta có 5 – x ≥ 0.
Û x ≤ 5.
Do đó tập B = (–∞; 5].
Để xác định tập hợp A \ B, ta vẽ sơ đồ sau đây:
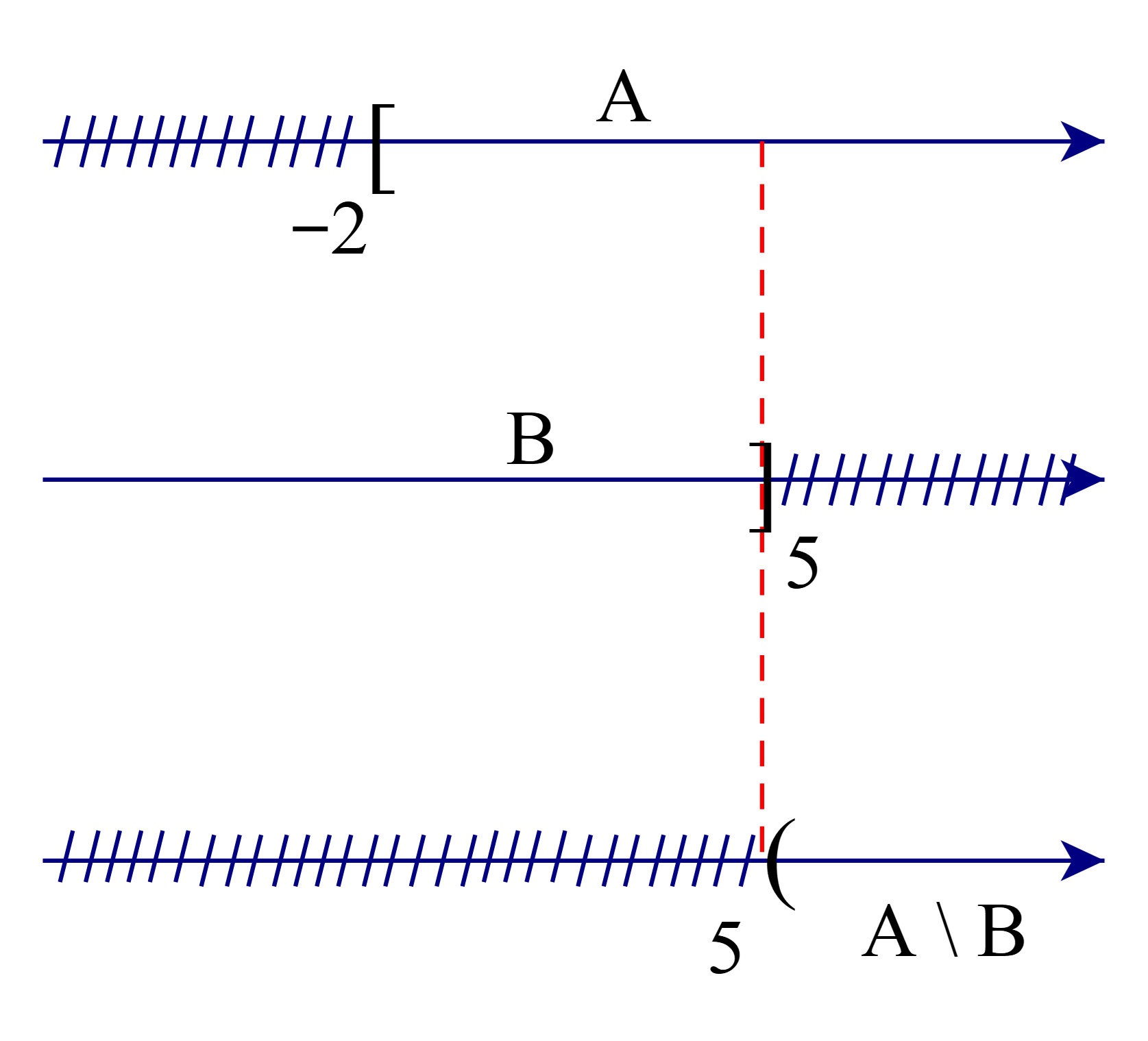
Từ sơ đồ, ta thấy A \ B = (5; +∞) (vì tập B có số 5 nên phần bù sẽ không lấy số 5).
Vậy ta chọn phương án C.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Cho tập hợp ; B là tập hợp tất cả các giá trị nguyên của b sao cho phương trình x2 – 2bx + 4 = 0 vô nghiệm. Số phần tử chung của hai tập hợp trên là:
Xem lời giải »
Câu 2:
Cho ba tập hợp A = [–2; 2], B = [1; 5], C = [0; 1]. Khi đó tập (A \ B) ∩ C là:
Xem lời giải »
Câu 3:
Cho hai tập khác rỗng A = (m – 1; 4], B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ ∅.
Xem lời giải »
Câu 4:
Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh?
Xem lời giải »


