Cho ∆ABC có C(–1; 2), đường cao BH: x – y + 2 = 0, đường phân giác trong AN: 2x – y + 5 = 0. Tọa độ điểm A là:
Câu hỏi:
Cho ∆ABC có C(–1; 2), đường cao BH: x – y + 2 = 0, đường phân giác trong AN: 2x – y + 5 = 0. Tọa độ điểm A là:
A.
B.
C.
D.
Trả lời:
Đáp án đúng là: A
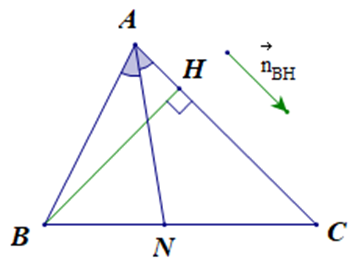
Đường cao BH: x – y + 2 = 0 có vectơ pháp tuyến là
Vì BH là đường cao của ∆ABC nên BH ⊥ AC.
Suy ra vectơ pháp tuyến của BH là vectơ chỉ phương của AC.
Do đó vectơ chỉ phương của AC là
Vì vậy AC có vectơ pháp tuyến là
Đường thẳng AC đi qua C(–1; 2), có vectơ pháp tuyến .
Suy ra phương trình AC: 1(x + 1) + 1(y – 2) = 0.
⇔ x + y – 1 = 0.
Ta có A là giao điểm của AC và AN.
Do đó tọa độ của điểm A là nghiệm của hệ phương trình:
Khi đó ta có
Vậy ta chọn phương án A.

