Cho hình chữ nhật ABCD, biết AB = 4a, AD = 3a. Tính độ dài vecto AB+AD

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho hình chữ nhật ABCD, biết AB = 4a, AD = 3a. Tính độ dài $\vec{A B} + \vec{A D}$ .

A. 7a

B. 6a

C. $2 a \sqrt{3}$

D. 5a

Trả lời:

Hướng dẫn giải

Đáp án đúng là: D

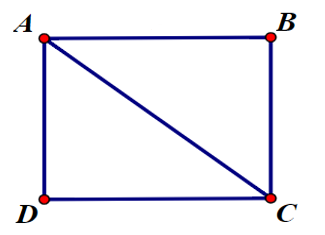
Cho hình chữ nhật ABCD, biết AB = 4a, AD = 3a. Tính độ dài vecto AB+AD (ảnh 1)

Vì ABCD là hình vuông nên BC = AD = 3a.

Theo quy tắc hình bình hành, ta có: $\vec{A B} + \vec{A D} = \vec{A C}$ .

Tam giác ABC vuông tại B: $A C^{2} = A B^{2} + B C^{2}$ (Định lý Pytago)

$\Leftrightarrow A C^{2} = 16 a^{2} + 9 a^{2} = 25 a^{2}$

⇒ AC = 5a.

Do đó $|\vec{A B} + \vec{A D}| = |\vec{A C}| = A C = 5 a$ .

Vậy ta chọn đáp án D.

Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:

Câu 1:

Cho 5 điểm M, N, P, Q, R. Tính tổng

\vec{M N} + \vec{P Q} + \vec{R N} + \vec{N P} + \vec{Q R}

Xem lời giải »

Câu 2:

Cho M, N, P lần lượt là trung điểm các cạnh AB, BC, CA của tam giác ABC. Hỏi vectơ $\vec{M P} + \vec{N P}$ bằng vectơ nào?

Xem lời giải »

Câu 3:

Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?

Xem lời giải »

Câu 4:

Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi M là trung điểm BC. Tính $\vec{A M} . \vec{B C}$ .

Xem lời giải »

Câu 5:

Cho tứ giác ABCD. Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh của tứ giác?

Xem lời giải »

Câu 6:

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm AB, CD. Khi đó $\vec{A C} + \vec{B D}$ bằng

Xem lời giải »

Câu 7:

Cho hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ cùng tác động vào một vật đứng tại điểm O, biết hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ đều có cường độ là 50 (N) và chúng hợp với nhau một góc 60°. Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?

Xem lời giải »

❮ Bài trước Bài sau ❯

Toán lớp 10 Chân trời sáng tạo

Cho hình chữ nhật ABCD, biết AB = 4a, AD = 3a. Tính độ dài vecto AB+AD

Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác: