Cho tam giác đều ABC cạnh a, điểm M là trung điểm của AC. Khẳng định nào sau đây là đúng
Câu hỏi:
Cho tam giác đều ABC cạnh a, điểm M là trung điểm của AC. Khẳng định nào sau đây là đúng?
B. ;
C. ;
D. .
Trả lời:
Đáp án đúng là: C
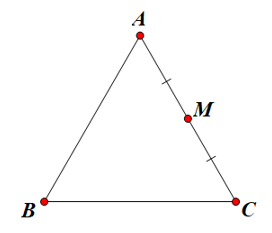
Do M là trung điểm của AC nên MA = MC = AC.
Suy ra:
• . Do đó phương án A là sai.
• . Do đó phương án B là sai.
Do ABC là tam giác đều nên AB = AC = a và
Tam giác ABC đều nên BM là trung tuyến cũng là đường cao.
Xét DABM vuông tại M có: BM = AB. sin A = a..
Suy ra:
• nên phương án C là đúng.
• nên phương án D là sai.
Vậy ta chọn phương án C.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Cho hình bình hành ABCD có tâm I. Có bao nhiêu vectơ khác có độ dài bằng độ dài của vectơ ?
Xem lời giải »
Câu 2:
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác và khác vectơ-không, cùng phương với có điểm đầu hoặc điểm cuối là các đỉnh của lục giác là:
Xem lời giải »
Câu 3:
Cho tam giác cân ABC tại A. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Cặp vectơ nào sau đây có độ dài bằng nhau?
Xem lời giải »
Câu 4:
Cho hình vẽ sau.
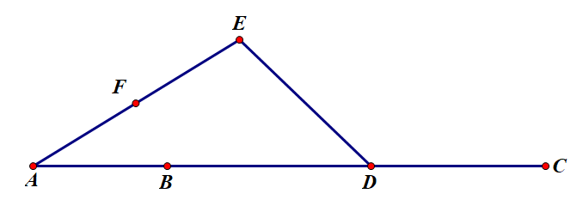
Hỏi trong hình có bao nhiêu vectơ khác cùng hướng với vectơ , có điểm đầu và điểm cuối là các điểm trong hình vẽ?
Xem lời giải »
Câu 5:
Cho hình thoi ABCD cạnh a và . Đẳng thức nào sau đây đúng?
Xem lời giải »

