Dây truyền đỡ trên cầu treo có dạng parabol ACB như hình vẽ. Đầu, cuối của dây được gắn vào các điểm A, B trên mỗi trục AA’ và BB’ với độ cao 30 m. Chiều dài A’B’ trên nền cầu bằng 200 m. Gọi

Dây truyền đỡ trên cầu treo có dạng parabol ACB như hình vẽ. Đầu, cuối của dây được gắn vào các điểm A, B trên mỗi trục AA’ và BB’ với độ cao 30 m. Chiều dài A’B’ trên nền cầu bằng 200 m. Gọi Q’, P’, H’, C’, I’, J’, K’ là các điểm chia đoạn A’B’ thành các phần bằng nhau (C’ chia đoạn A’B’ thành hai phần bằng nhau). Các thanh thẳng đứng nối nền cầu với đáy dây truyền: QQ’, PP’, HH’, CC’, II’, JJ’, KK’ gọi là các dây cáp treo.

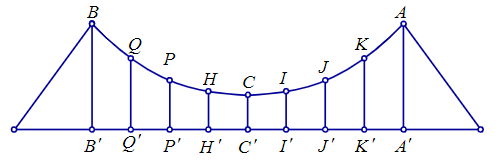
Biết độ cao ngắn nhất của dây truyền trên cầu là C’C = 5 m. Tổng độ dài của các dây cáp treo là:

Hướng dẫn giải

Đáp án đúng là: C

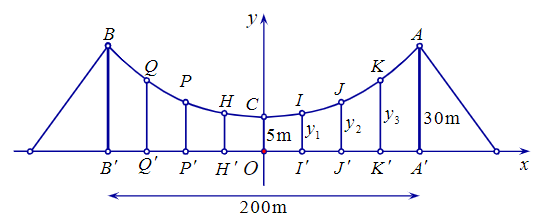
Giả sử parabol có dạng y = ax² + bx + c, với a ≠ 0.

Chọn hệ trục Oxy như hình vẽ. Khi đó O ≡ C’ là trung điểm A’B’.

Suy ra OA = OB = 100 (m).

Do đó parabol đi qua điểm A(100; 30).

Suy ra 30 = a.100² + b.100 + c.

Khi đó 10 000a + 100b + c = 30    (1)

Khi chọn hệ trục Oxy như hình vẽ, ta có Oy là trục đối xứng của parabol.

Vì C là giao điểm của trục đối xứng Oy và parabol.

Nên C là đỉnh của parabol.

Parabol có đỉnh C(0; 5).

Ta suy ra 5 = a.0² + b.0 + c.

Do đó c = 5

Ta có x_C = 0.

Suy ra \(\frac{{ - b}}{{2a}} = 0\).

Do đó b = 0.

Thay b = 0, c = 5 vào (1) ta được 10 000a + 100.0 + 5 = 30.

Suy ra a = \(\frac{1}{{400}} \ne 0\).

Vậy parabol có hàm số \(y = \frac{1}{{400}}{x^2} + 5\).

Đoạn A’B’ được chia thành 8 phần bằng nhau.

Suy ra OI’ = I’J’ = J’K’ = \(\frac{{200}}{8}\) = 25 (m).

Khi đó ta có \(\left\{ \begin{array}{l}OI' = 25\\OJ' = 25.2 = 50\\OK' = 25.3 = 75\end{array} \right.\)

Do đó x_I’ = 25, x_J’ = 50, x_K’ = 75.

Với x_I’ = 25, ta có \({y_1} = {y_{I'}} = \frac{1}{{400}}{.25^2} + 5 = \frac{{105}}{{16}}\).

Với x_J’ = 50, ta có \({y_2} = {y_{J'}} = \frac{1}{{400}}{.50^2} + 5 = \frac{{45}}{4}\).

Với x_K’ = 75, ta có \({y_3} = {y_{K'}} = \frac{1}{{400}}{.75^2} + 5 = \frac{{305}}{{16}}\).

Vậy tổng độ dài của các dây cáp treo bằng:

OC + 2y₁ + 2y₂ + 2y₃

\( = 5 + 2.\frac{{105}}{{16}} + 2.\frac{{45}}{4} + 2.\frac{{305}}{{16}} = \frac{{315}}{4} = 78,75\) (m)

Vậy ta chọn phương án C.