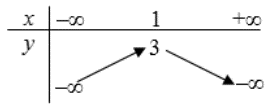
Đồ thị hàm số y = –x^2 + 2x + 3 cắt trục hoành tại mấy điểm? A. 0; B. 3; C. 1; D. 2.
Câu hỏi:
Đồ thị hàm số y = –x2 + 2x + 3 cắt trục hoành tại mấy điểm?
A. 0;
B. 3;
C. 1;
D. 2.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Cách 1:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 2, c = 3.
∆ = b2 – 4ac = 22 – 4.(–1).3 = 16 > 0.
Suy ra phương trình –x2 + 2x + 3 = 0 có 2 nghiệm x1, x2 phân biệt.
Vì vậy đồ thị hàm số bậc hai y = –x2 + 2x + 3 cắt trục hoành tại hai điểm lần lượt có hoành độ là x1, x2.
Vậy ta chọn phương án D.
Cách 2:
Vẽ đường thẳng y = 0 biểu diễn như trong hình dưới đây:
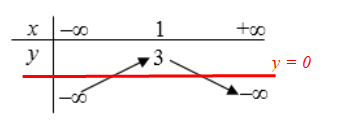
Do đó đồ thị hàm số cắt trục hoành (y = 0) tại hai điểm phân biệt.
