Giải Toán 10 trang 124 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 124 Tập 1 trong Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 124.

Giải Toán 10 trang 124 Tập 1 Chân trời sáng tạo

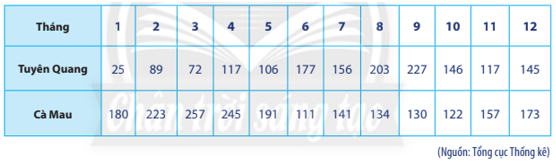
Vận dụng 2 trang 124 Toán lớp 10 Tập 1: Bảng dưới đây thống kê tổng số giờ nắng trong năm 2019 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở Tuyên Quang và Cà Mau.

a) Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh.

b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh.

Lời giải:

a)

* Tỉnh Tuyên Quang:

+ Số trung bình:

$\overline{x_1}=\frac{25+89+72+117+106+177+156+203+227+146+117+145}{12}\approx 131,67$

+ Phương sai mẫu số liệu ở tỉnh Tuyên Quang là:

$S_1^2=\frac{1}{12}\left({25}^2+{89}^2+{72}^2+{117}^2+{106}^2+{177}^2+{156}^2+{203}^2+{227}^2+{146}^2+{117}^2+{145}^2\right)-{\left(131,67\right)}^2$

 ≈ 2920,34.

+ Độ lệch chuẩn mẫu số liệu ở tỉnh Tuyên Quang là:

S₁ = $\sqrt{S_1^2}=\sqrt{2920,34}\approx 54,04$.

* Tỉnh Cà Mau:

+ Số trung bình:

$\overline{x_2}=\frac{180+223+257+245+191+111+141+134+130+122+157+173}{12}=172$

+ Phương sai mẫu số liệu ở tỉnh Cà Mau là:

$S_2^2=\frac{1}{12}$(180² + 223² + 257² + 245² + 191² + 111² + 141² + 134² + 130² + 122² + 157² + 173²) – 172² = 2183.

+ Độ lệch chuẩn mẫu số liệu ở tỉnh Cà Mau là:

S₂ = $\sqrt{S_2^2}=\sqrt{2183}\approx 46,72$.

b) Phương sai mẫu và độ lệch chuẩn mẫu số liệu ở tỉnh Tuyên Quang cao hơn tỉnh Cà Mau nên tổng số giờ nắng trong năm 2019 theo từng tháng ở tỉnh Tuyên Quang có độ phân tán cao hơn ở tỉnh Cà Mau. Do đó, sự thay đổi tổng số giờ nắng theo từng tháng ở tỉnh Cà Mau ổn định (có ít sự thay đổi) hơn so với tỉnh Tuyên Quang.

Bài 1 trang 124 Toán lớp 10 Tập 1: Hãy chọn ngẫu nhiên trong lớp ra 5 bạn nam và 5 bạn nữ rồi đo chiều cao các bạn đó. So sánh xem chiều cao của các bạn nam hay các bạn nữ đồng đều hơn.

Lời giải:

Kết quả của bài tập này phụ thuộc vào chiều cao của các bạn nam và nữ mà bạn chọn ra.

Chẳng hạn, ta có ví dụ sau:

+ Chọn ra 5 bạn nam có chiều cao lần lượt là: 162 cm; 157 cm; 169 cm; 170 cm; 165 cm.

+ Chọn ra 5 bạn nữ có chiều cao lần lượt là: 150 cm; 163 cm; 155 cm; 160 cm; 169 cm.

Ta đi tính khoảng biến thiên, khảng tứ phân vị, phương sai mẫu và độ lệch chuẩn của từng mẫu số liệu rồi so sánh.

+ Sắp xếp các số liệu chiều cao nam theo thứ tự không giảm, ta được:

157; 162; 165; 169; 170.

Khoảng biến thiên chiều cao của nam: R₁ = 170 – 157 = 13.

Vì cỡ mẫu là 5 là số lẻ nên tứ phân vị thứ hai là Q₂ = 165.

Tứ phân vị thứ nhất là trung vị của mẫu: 157; 162. Do đó Q₁ = 159,5.

Tứ phân vị thứ ba là trung vị của mẫu: 169; 170. Do đó Q₃ = 169,5.

Khoảng tứ phân vị ∆_Q = 169,5 – 159,5 = 10. 

Chiều cao trung bình của nam là:

$\overline{x_1}=\frac{162+157+169+170+165}{5}=164,6$

Phương sai mẫu số liệu chiều cao của nam là:

$S_1^2=\frac{1}{5}$(162² + 157² + 169² + 170² + 165²) – (164,6)² = 22,64.

Độ lệch chuẩn mẫu số liệu chiều cao của nam là:

S₁ = $\sqrt{S_1^2}=\sqrt{22,64}\approx 4,76$.

+ Sắp xếp các số liệu chiều cao nữ theo thứ tự không giảm, ta được:

150; 155; 160; 163; 169.

Khoảng biến thiên chiều cao của nữ: R₂ = 169 – 150 = 19.

Vì cỡ mẫu là 5 là số lẻ nên tứ phân vị thứ hai là Q'₂ = 160.

Tứ phân vị thứ nhất là trung vị của mẫu: 150; 155. Do đó Q'₁ = 152,5.

Tứ phân vị thứ ba là trung vị của mẫu: 163; 169. Do đó Q'₃ = 166.

Khoảng tứ phân vị ∆'_Q = 166 – 152,5 = 13,5. 

Chiều cao trung bình của nữ là:

$\overline{x_2}=\frac{150+163+155+160+169}{5}=159,4$

Phương sai mẫu số liệu chiều cao của nữ là:

$S_2^2=\frac{1}{5}$(150² + 163² + 155² + 160² + 169²) – (159,4)² = 42,64.

Độ lệch chuẩn mẫu số liệu chiều cao của nữ là:

S₂ = $\sqrt{S_2^2}=\sqrt{42,64}\approx 6,53$.

Từ đó ta thấy khoảng biến thiên, khoảng tứ phân vị, phương sai mẫu và độ lệch chuẩn mẫu số liệu chiều cao của nam đều thấp hơn của nữ. Điều đó cho ta biết rẳng chiều cao của nam có độ phân tán thấp hơn chiều cao của nữ ở mẫu số liệu trên. Do đó, chiều cao của các bạn nam đồng đều hơn so chiều cao của các bạn nữ.

Bài 2 trang 124 Toán lớp 10 Tập 1: Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và các giá trị ngoại lệ của các mẫu số liệu sau:

a) 6; 8; 3; 4; 5; 6; 7; 2; 4.

b) 13; 37; 64; 12; 26; 43; 29; 23.

Lời giải:

a) Số trung bình: $\overline{x}=\frac{6+8+3+4+5+6+7+2+4}{9}=5$.

Phương sai mẫu số liệu là:

$S^2=\frac{1}{9}$(6² + 8² + 3² + 4² + 5² + 6² + 7² + 2² + 4²) – 5² = .

Độ lệch chuẩn mẫu số liệu là: $S=\sqrt{S^2}=\sqrt{\frac{10}{3}}=\frac{\sqrt{30}}{3}$.

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

2; 3; 4; 4; 5; 6; 6; 7; 8.

Khoảng biến thiên của mẫu là: R = 8 – 2 = 6.

Vì cỡ mẫu là 9 là số lẻ nên tứ phân vị thứ hai là Q₂ = 5.

Tứ phân vị thứ nhất là trung vị của mẫu: 2; 3; 4; 4. Do đó Q₁ = 3,5.

Tứ phân vị thứ ba là trung vị của mẫu: 6; 6; 7; 8. Do đó Q₃ = 6,5.

Khoảng tứ phân vị của mẫu là: ∆_Q = 6,5 – 3,5 = 3.

Ta có: Q₃ + 1,5∆_Q = 6,5 + 1,5 . 3 = 11 và Q₁ – 1,5∆_Q = 3,5 – 1,5 . 3 = – 1.

Do đó mẫu số liệu không có giá trị ngoại lệ.

b)

Số trung bình: $\overline{x}=\frac{13+37+64+12+26+43+29+23}{8}=30,875$.

Phương sai mẫu số liệu là: $S=\sqrt{S^2}=\sqrt{255,86}\approx 16$

$S^2=\frac{1}{8}$(13² + 37² + 64² + 12² + 26² + 43² + 29² + 23²) – (30,875)² ≈ 255,86.

Độ lệch chuẩn mẫu số liệu là: .

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

12; 13; 23; 26; 29; 37; 43; 64.

Khoảng biến thiên của mẫu là: R = 64 – 12 = 52.

Vì cỡ mẫu là 8 là số chẵn nên tứ phân vị thứ hai là Q₂ = $\frac{1}{2}\left(26+29\right)=27,5$.

Tứ phân vị thứ nhất là trung vị của mẫu: 12; 13; 23; 26. Do đó Q₁ = 18.

Tứ phân vị thứ ba là trung vị của mẫu: 29; 37; 43; 64. Do đó Q₃ = 40.

Khoảng tứ phân vị của mẫu là: ∆_Q = 40 – 18 = 22.

Ta có: Q₃ + 1,5∆_Q = 40 + 1,5 . 22 = 73 và Q₁ – 1,5∆_Q = 18 – 1,5 . 22 = – 15.

Do đó mẫu số liệu không có giá trị ngoại lệ.

Lời giải bài tập Toán lớp 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 120

• Giải Toán 10 trang 121

• Giải Toán 10 trang 122

• Giải Toán 10 trang 125