Giải Toán 10 trang 125 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 125 Tập 1 trong Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 125.

Giải Toán 10 trang 125 Tập 1 Chân trời sáng tạo

Bài 3 trang 125 Toán lớp 10 Tập 1: Hãy tìm độ lệch chuẩn, khoảng biến thiên và khoảng tứ phân vị của các mẫu số liệu sau:

a)

b)

Giá trị	0	1	2	3	4
Tần suất	0,1	0,2	0,4	0,2	0,1

Lời giải:

a) Cỡ mẫu n = 10 + 20 + 30 + 20 + 10 = 90.

Số trung bình: $\overline{x}=\frac{10.\left(-2\right)+20.\left(-1\right)+30.0+20.1+10.2}{90}=0$.

Phương sai mẫu số liệu là:

S² = $\frac{1}{90}$[10 . (– 2)² + 20 . (– 1)² + 30 . 0² + 20 . 1² + 10 . 2²] – 0² = $\frac{4}{3}$.

Độ lệch chuẩn mẫu số liệu là:

S = $\sqrt{S^2}=\sqrt{\frac{4}{3}}=\frac{2\sqrt{3}}{3}$.

Sắp xếp các số liệu của mẫu theo thứ tự không giảm, ta được:

– 2; – 2; – 2; – 2 ; – 2; – 2; – 2; – 2; – 2; – 2; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2.

Khoảng biến thiên của mẫu số liệu là: R = 2 – (– 2) = 4.

Vì cỡ mẫu là 90 là số chẵn nên tứ phân vị thứ hai là Q₂ = 0.

Tứ phân vị thứ nhất là trung vị của mẫu: – 2; – 2; – 2; – 2 ; – 2; – 2; – 2; – 2; – 2; – 2; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; – 1; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0. Do đó Q₁ = – 1.

Tứ phân vị thứ ba là trung vị của mẫu: 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2. Do đó Q₃ = 1.

Khoảng tứ phân vị là ∆_Q = 1 – (– 1) = 2.

b) Số trung bình:  = 0,1 . 0 + 0,2 . 1 + 0,4 . 2 + 0,2 . 3 + 0,1 . 4 = 2.

Phương sai mẫu số liệu là:

S² = (0,1 . 0² + 0,2 . 1² + 0,4 . 2² + 0,2 . 3² + 0,1 . 4²) – 2² = 1,2.

Độ lệch chuẩn mẫu số liệu là:

S = $\sqrt{S^2}=\sqrt{1,2}=\frac{\sqrt{30}}{5}$.

Giả sử cỡ mẫu là 10. Khi đó:

Tần số của giá trị 0 là 0,1 . 10 = 1.

Tần số của giá trị 1 là 0,2 . 10 = 2.

Tần số của giá trị 2 là 0,4 . 10 = 4.

Tần số của giá trị 3 là 0,2 . 10 = 2.

Tần số của giá trị 4 là 0,1 . 1 = 1.

Sắp xếp các số liệu của mẫu theo thứ tự không giảm, ta được:

0; 1; 1; 2; 2; 2; 2; 3; 3; 4.

Khoảng biến thiên của mẫu số liệu là R = 4 – 0 = 4.

Vì cỡ mẫu là số chẵn nên tứ phân vị thứ hai là Q₂ = 2.

Tứ phân vị thứ nhất là trung vị của mẫu: 0; 1; 1; 2; 2. Do đó Q₁ = 1.

Tứ phân vị thứ ba là trung vị của mẫu: 2; 2; 3; 3; 4. Do đó Q₃ = 3.

Khoảng tứ phân vị là: ∆_Q = 3 – 1 = 2.

Bài 4 trang 125 Toán lớp 10 Tập 1: Hãy so sánh số trung bình, phương sai và độ lệch chuẩn của ba mẫu số liệu sau:

Mẫu 1:         0,1;    0,3;   0,5;    0,5;    0,3;    0,7.

Mẫu 2:         1,1;    1,3;    1,5;    1,5;    1,3;    1,7.

Mẫu 3:         1;       3;       5;       5;       3;       7.

Lời giải:

+ Số trung bình: $\overline{x_1}=\frac{0,1+0,3+0,5+0,5+0,3+0,7}{6}=0,4$.

+ Phương sai mẫu: $S_1^2=\frac{1}{6}$(0,1² + 0,3² + 0,5² + 0,5² + 0,3² + 0,7²) – 0,4² = $\frac{11}{300}$.

+ Độ lệch chuẩn: $S_1=\sqrt{S_1^2}=\sqrt{\frac{11}{300}}=\frac{\sqrt{33}}{30}$.

* Mẫu 2:

+ Số trung bình: $\overline{x_2}=\frac{1,1+1,3+1,5+1,5+1,3+1,7}{6}=1,4$.

+ Phương sai mẫu: $S_2^2=\frac{1}{6}$(1,1² + 1,3² + 1,5² + 1,5² + 1,3² + 1,7²) – 1,4² = $\frac{11}{300}$.

+ Độ lệch chuẩn: $S_2=\sqrt{S_2^2}=\sqrt{\frac{11}{300}}=\frac{\sqrt{33}}{30}$.

* Mẫu 3:

+ Số trung bình: $\overline{x_3}=\frac{1+3+5+5+3+7}{6}=4$.

+ Phương sai mẫu: $S_3^2=\frac{1}{6}$(1² + 3² + 5² + 5² + 3² + 7²) – 4² = $\frac{11}{3}$.

+ Độ lệch chuẩn: $S_3=\sqrt{S_3^2}=\sqrt{\frac{11}{3}}=\frac{\sqrt{33}}{3}$.

* So sánh ta thấy:

+ Phương sai mẫu và độ lệch chuẩn của mẫu 1 và mẫu 2 là như nhau. Số trung bình của mẫu 1 nhỏ hơn số trung bình của mẫu 2.

+ Số trung bình, độ lệch chuẩn của mẫu 3 gấp 10 lần mẫu 1, phương sai mẫu 3 gấp 100 lần phương sai mẫu 1.

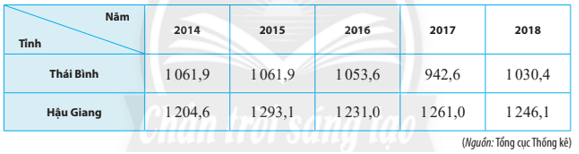
Bài 5 trang 125 Toán lớp 10 Tập 1: Sản lượng lúa các năm từ 2014 đến 2018 của hai tỉnh Thái Bình và Hậu Giang được cho ở bảng sau (đơn vị: nghìn tấn).

a) Hãy tính độ lệch chuẩn và khoảng biến thiên của sản lượng lúa từng tỉnh.

b) Tỉnh nào có sản lượng lúa ổn định hơn? Tại sao?

Lời giải:

a)

* Tỉnh Thái Bình:

Số trung bình: $\overline{x_1}=\frac{1061,9+1061,9+1053,6+942,6+1030,4}{5}=1030,08$.

Phương sai mẫu:

$S_1^2=\frac{1}{5}$(1061,9² + 1061,9² + 1053,6² + 942,6² + 1030,4²) – 1030,08² ≈ 2046,21.

Độ lệch chuẩn: S₁ = $\sqrt{S_1^2}=\sqrt{2046,21}\approx 45,24$.

Khoảng biến thiên: R₁ = 1061,9 – 942,6 = 119,3.

* Tỉnh Hậu Giang:

Số trung bình: $\overline{x_2}=\frac{1204,6+1293,1+1231,0+1261,0+1246,1}{5}=1247,16$.

Phương sai mẫu:

$S_2^2=\frac{1}{5}$(1204,6² + 1293,1² + 1231,0² + 1261,0² + 1246,1²) – 1247,16² = 875,1304.

Độ lệch chuẩn: S₂ = $\sqrt{S_2^2}=\sqrt{875,1304}\approx 29,58$.

Khoảng biến thiên: R₂ = 1293,1 – 1204,6 = 88,5.

b) Do 45,24 > 29,58, 119,3 > 88,5 nên độ lệch chuẩn, khoảng biến thiên của sản lượng lúa tỉnh Thái Bình lớn hơn tỉnh Hậu Giang, điều đó có nghĩa là sản lượng lúa của tỉnh Thái Bình trong các năm từ 2014 đến 2018 có độ phân tán cao hơn tỉnh Hậu Giang.

Vậy tỉnh Hậu Giang có sản lượng lúa ổn định hơn (ít bị phân tán hơn).

Bài 6 trang 125 Toán lớp 10 Tập 1: Kết quả điều tra mức lương hằng tháng của một số công nhân của hai nhà máy A và B được cho ở bảng sau (đơn vị: triệu đồng):

a) Hãy tìm số trung bình, mốt, tứ phân vị và độ lệch chuẩn của hai mẫu số liệu lấy từ nhà máy A và nhà máy B.

b) Hãy tìm các giá trị ngoại lệ trong mỗi mẫu số liệu trên. Công nhân nhà máy nào có mức lương cao hơn? Tại sao?

Lời giải:

a)

* Nhà máy A:

+ Số trung bình mức lương hàng tháng: $\overline{x_A}=\frac{4+5+5+47+5+6+4+4}{8}=10$.

+ Giá trị 4 và 5 có tần số lớn nhất nên mốt của mẫu số liệu ở nhà máy A là 4 và 5.

+ Sắp xếp các số liệu theo thứ tự không giảm, ta được:

4; 4; 4; 5; 5; 5; 6; 47.

Vì cỡ mẫu là 8 là số chẵn nên tứ phân vị thứ hai là Q_2A = 5.

Tứ phân vị thứ nhất là trung vị của mẫu: 4; 4; 4; 5. Do đó Q_1A = 4.

Tứ phân vị thứ ba là trung vị của mẫu: 5; 5; 6; 47. Do đó Q_3A = 5,5.

+ Phương sai mẫu:

$S_A^2=\frac{1}{8}$(4² + 5² + 5² + 47² + 5² + 6² + 4² + 4²) – 10² = 196.

+ Độ lệch chuẩn: S_A = $\sqrt{S_A^2}=\sqrt{196}=14$.

* Nhà máy B:

+ Số trung bình mức lương hàng tháng: $\overline{x_B}=\frac{2+9+9+8+10+9+9+11+9}{9}\approx 8,4$.

+ Giá trị 9 có tần số lớn nhất nên mốt của mẫu số liệu ở nhà máy B là 9.

+ Sắp xếp các số liệu theo thứ tự không giảm, ta được:

2; 8; 9; 9; 9; 9; 9; 10; 11.

Vì cỡ mẫu là 9 là số lẻ nên tứ phân vị thứ hai là Q_2B = 9.

Tứ phân vị thứ nhất là trung vị của mẫu: 2; 8; 9; 9. Do đó Q_1B = 8,5.

Tứ phân vị thứ ba là trung vị của mẫu: 9; 9; 10; 11. Do đó Q_3B = 9,5.

+ Phương sai mẫu:

$S_B^2=\frac{1}{9}$(2² + 8² + 9² + 9² + 9² + 9² + 9² + 10² + 11²) – 8,4² = 6,55.

+ Độ lệch chuẩn: S_B = $\sqrt{S_B^2}=\sqrt{6,55}\approx 2,6$.

b)

+ Khoảng tứ phân vị của mẫu số liệu ở nhà máy A là: ∆_QA = 5,5 – 4 = 1,5.

Ta có: Q_3A + 1,5∆_QA = 5,5 + 1,5 . 1,5 = 7,75 và Q_1A – 1,5∆_QA = 4 – 1,5 . 1,5 = 1,75.

Do đó giá trị ngoại lệ trong mẫu số liệu ở nhà máy A là 47.

+ Khoảng tứ phân vị của mẫu số liệu ở nhà máy B là: ∆_QB = 9,5 – 8,5 = 1.

Ta có: Q_3B + 1,5∆_QB = 9,5 + 1,5 . 1 = 11 và Q_1B – 1,5∆_QB = 8,5 – 1,5 . 1 = 7.

Do đó giá trị ngoại lệ trong mẫu số liệu ở nhà máy B là 2.

+ Quan sát các số liệu tính được ở câu a), ta thấy

- Số trung bình mức lương hàng tháng của công nhân ở nhà máy A cao hơn nhà máy B.

- Phương sai mẫu và độ lệch chuẩn mẫu số liệu ở nhà máy A cao hơn nhà máy B nên mức lương hằng tháng của công nhân nhà máy A có độ phân tán cao hơn nhà máy B, do đó mức lương của công nhân nhà máy B ổn định hơn nhà máy A.

- Mức lương xuất hiện nhiều nhất trong mẫu A là 4 và 5 triệu đồng, nhà máy B là 9 triệu đồng.

Do đó, ta có thể khẳng định công nhân nhà máy A có mức lương cao hơn (đều và ổn định hơn).

Lời giải bài tập Toán lớp 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 120

• Giải Toán 10 trang 121

• Giải Toán 10 trang 122

• Giải Toán 10 trang 124