Giải Toán 10 trang 32 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 32 Tập 1 trong Bài 1: Bất phương trình bậc nhất hai ẩn Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 32.

Giải Toán 10 trang 32 Tập 1 Chân trời sáng tạo

Thực hành 3 trang 32 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của các bất phương trình sau :

a) 2x + y – 2 ≤ 0   

b) x – y –  2 ≥ 0

Lời giải:

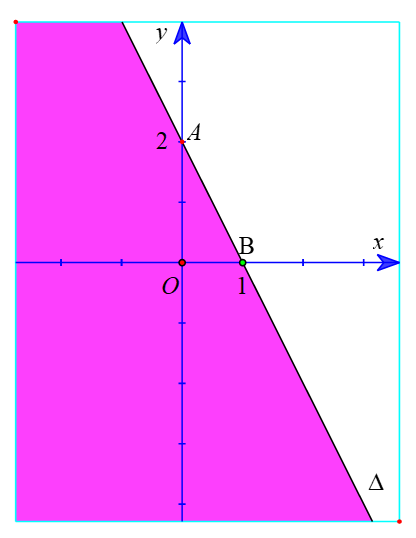
a) Vẽ đường thẳng ∆ : 2x + y – 2 =  0 đi qua hai điểm A(0; 2); B( 1; 0).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và  2 . 0 + 0 – 2 < 0.

Suy ra (0 ; 0) là nghiệm của bất phương trình 2x + y – 2 ≤ 0.

Do đó, miền nghiệm của bất phương trình 2x + y – 2 ≤ 0 là nửa mặt phẳng kể cả bờ ∆, có chứa gốc O (là miền tô màu trong hình sau).

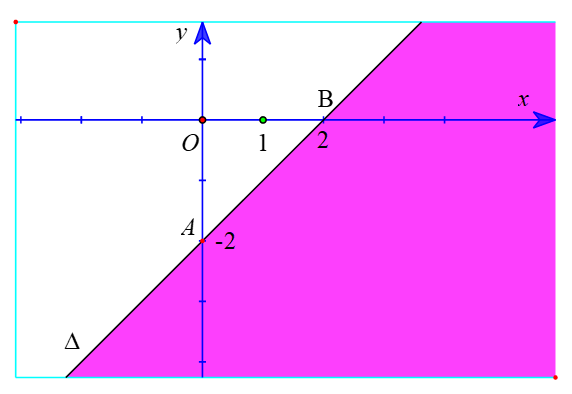
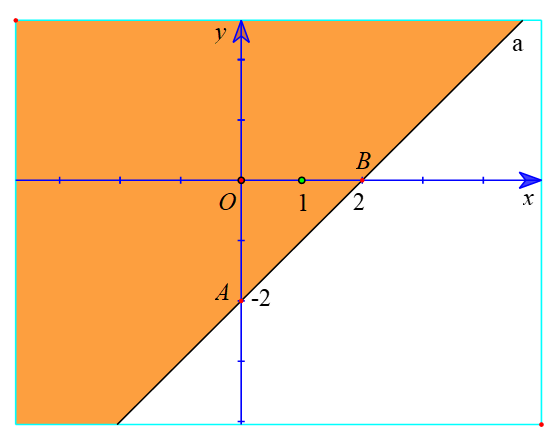
b) Vẽ đường thẳng ∆ : x –  y – 2 =  0 đi qua hai điểm A(0; – 2); B(2; 0).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và  0 –  0 – 2 < 0.

Suy ra (0 ; 0) không phải là nghiệm của bất phương trình x –  y – 2 ≥ 0.

Do đó, miền nghiệm của bất phương trình x –  y – 2 ≥ 0 là nửa mặt phẳng kể cả bờ ∆, không chứa điểm O (là miền được tô màu trong hình sau).

Vận dụng 2 trang 32 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của hai bất phương trình sau trên cùng một mặt phẳng tọa độ Oxy.

a) y ≥ 2

b) x ≤ 4.

Lời giải:

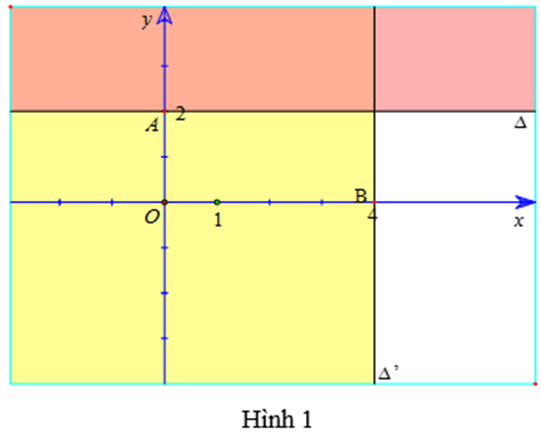
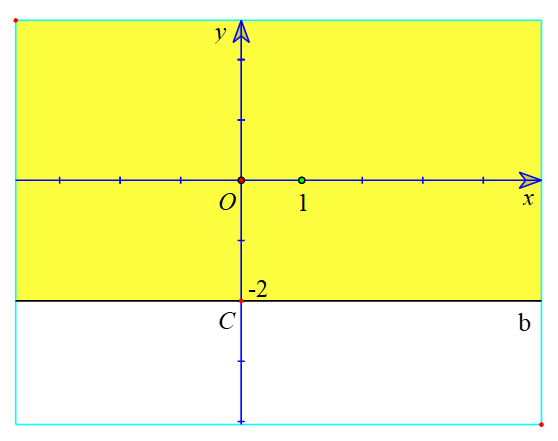
a) Từ y ≥ 2 suy ra y – 2 ≥  0.

Vẽ đường thẳng ∆ : y – 2 =  0 (đường thẳng đi qua A(0 ; 2) và song song với Ox).

Xét gốc tọa độ O(0 ; 0).

Ta thấy O ∉ ∆ và  0 – 2 = –2 < 0.

Suy ra (0 ; 0) không phải là nghiệm của bất phương trình y – 2 ≥  0.

Do đó, miền nghiệm của bất phương trình y – 2 ≥  0 là nửa mặt phẳng kể cả bờ ∆, không chứa điểm O (là miền tô màu đỏ trong hình 1).

b) Tương tự, từ x ≤ 4 suy ra bất phương trình x – 4 ≤ 0.

Vẽ đường thẳng ∆’ : x – 4 =  0 (đường thẳng đi qua B(4 ; 0) và song song với Oy).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆’ và  0 – 4 = –4 < 0.

Suy ra (0 ; 0) là nghiệm của bất phương trình x – 4 ≤ 0.

Do đó, miền nghiệm của bất phương trình x – 4 ≤ 0 là nửa mặt phẳng kể cả bờ ∆’, có chứa điểm O (là miền tô màu vàng trong hình 1).

Bài 1 trang 32 Toán lớp 10 Tập 1: Cho bất phương trình bậc nhất hai ẩn x -  2y + 6 > 0.

a) (0 ; 0) có phải là một nghiệm của bất phương trình đã cho không ?

b) Chỉ ra ba cặp số (x ; y) là nghiệm của bất phương trình đã cho.

c) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng tọa độ Oxy.

Lời giải:

a) Với cặp (0 ; 0) ta có : 0 – 2.0 + 6  = 6 > 0 nên (0 ; 0) là nghiệm của bất phương trình đã cho.

Vậy (0 ; 0) là một nghiệm của bất phương trình x -  2y + 6 > 0.

b)

+ Lấy cặp số (1 ; 0) ta có 1 – 2.0 + 6 = 7 > 0 nên cặp số (1 ; 0) là một nghiệm của bất phương trình x -  2y + 6 > 0.

+ Lấy cặp số (0 ; 1) ta có 0 – 2.1 + 6 = 4 > 0 nên cặp số (0 ; 1) là một nghiệm của bất phương trình x -  2y + 6 > 0.

+ Lấy cặp số (-1 ; -1) ta có –1 – 2. (–1) + 6 = 7 > 0 nên cặp số (-1 ; -1) là một nghiệm của bất phương trình x -  2y + 6 > 0.

Vậy ta có ba cặp số (1 ; 0) ; (0 ; 1) ; (-1 ; -1) đều là nghiệm của bất phương trình x -  2y + 6 > 0.

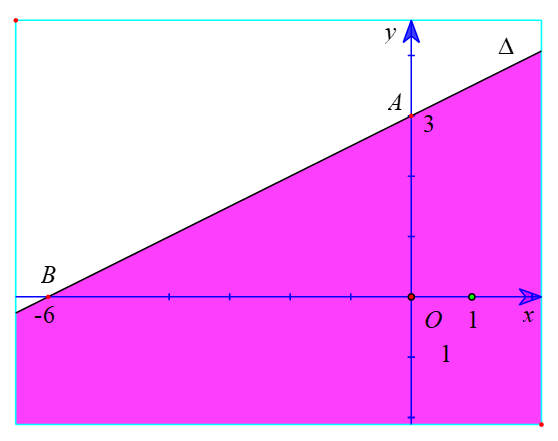
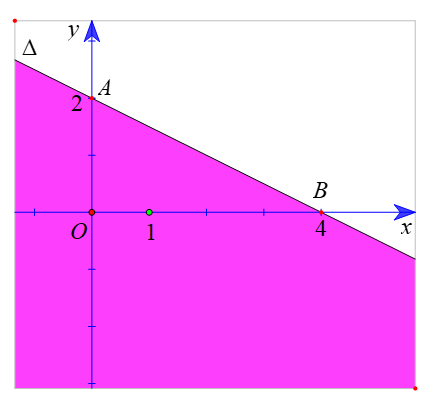
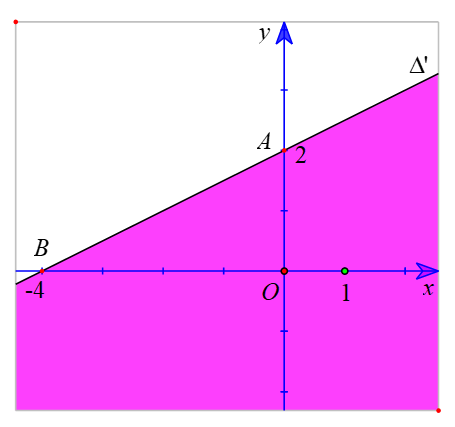
c) Vẽ đường thẳng ∆ : x –  2y + 6 =  0 đi qua hai điểm A(0; 3); B(-6; 0).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và  (0 ; 0) là một nghiệm của bất phương trình

x -  2y + 6 > 0.

Do đó, miền nghiệm của bất phương trình x -  2y + 6 > 0 là nửa mặt phẳng không kể bờ ∆, chứa điểm O (là miền được tô màu trong hình sau).

Bài 2 trang 32 Toán lớp 10 Tập 1: Biểu diễn tập nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy.

a) – x + y + 2 > 0

b) y + 2 ≥ 0

c ) – x + 2 ≤ 0.

Lời giải:

a) Vẽ đường thẳng a : – x + y + 2 = 0 đi qua hai điểm A(0; - 2); B(2; 0).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ a và  –  0 + 0 + 2 = 2 > 0.

Suy ra (0 ; 0) là một nghiệm của bất phương trình  – x + y + 2 > 0.

Do đó, miền nghiệm của bất phương trình – x + y + 2 > 0 là nửa mặt phẳng không kể bờ a, chứa điểm O (là miền tô màu trong hình sau).

b) Vẽ đường thẳng b : y + 2 = 0 đi qua điểm C(0; -2) và song song với trục Ox

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ b và  0 + 2 = 2 > 0

Suy ra (0 ; 0)  là nghiệm của bất phương trình y + 2 ≥ 0.

Do đó, miền nghiệm của bất phương trình y + 2 ≥ 0 là nửa mặt phẳng kể cả bờ b, chứa điểm O (là miền tô màu vàng trong hình sau).

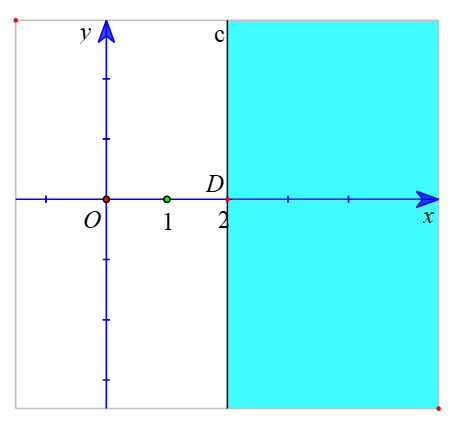
c) ) Vẽ đường thẳng c : – x + 2 = 0.đi qua điểm D (2; 0) và song song với trục Oy.

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ c và – 0 + 2 = 2 > 0

 Suy ra (0 ; 0) không là nghiệm của bất phương trình – x + 2 ≤ 0.

Do đó, miền nghiệm của bất phương trình – x + 2 ≤ 0.là nửa mặt phẳng kể cả  bờ c, không chứa điểm O (là miền tô màu xanh trong hình sau).

Bài 3 trang 32 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ oxy

a) – x + 2 + 2(y – 2) < 2(1 – x)

b) 3(x – 1 ) + 4(y – 2) < 5x – 3.

Lời giải:

a) Ta có: – x + 2 + 2(y – 2 ) < 2(1 – x)

⇔ – x + 2 + 2(y – 2 ) – 2(1 – x) < 0

⇔ – x + 2 + 2y – 4  – 2 + 2x < 0

⇔ x + 2y – 4 < 0

Ta sẽ biểu diễn miền nghiệm của bất phương trình x + 2y – 4 < 0.

Vẽ đường thẳng ∆: x + 2y – 4 = 0 đi qua điểm A(0; 2) và B (4 ; 0).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và  0 + 2.0 – 4 = – 4 < 0.

Suy ra (0 ; 0) là nghiệm của bất phương trình x + 2y – 4 < 0.

Do đó, miền nghiệm của bất phương trình x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ ∆, chứa điểm O (là miền tô màu trong hình sau).

b) Ta có: 3(x – 1 ) + 4(y – 2) < 5x – 3

⇔ 3x – 3  + 4y – 8 – 5x + 3 < 0

⇔ –  2x + 4y – 8 < 0

⇔ – x + 2y – 4 < 0

Ta sẽ biểu diễn miền nghiệm của bất phương trình – x + 2y – 4 < 0

Vẽ đường thẳng ∆’ : – x + 2y – 4 = 0 đi qua điểm A(0; 2) và B (– 4 ; 0).

Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆’ và  – 0 + 2. 0 – 4 = – 4 < 0.

Suy ra (0 ; 0) là nghiệm của bất phương trình  – x + 2y – 4 < 0.

Do đó, miền nghiệm của bất phương trình –x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ ∆’, chứa điểm O (là miền tô màu trong hình sau).

Bài 4 trang 32 Toán lớp 10 Tập 1: Bạn Cúc muốn pha hai loại nước cam. Để pha một lít nước cam loại I cần 30 g bột cam, còn một lít nước cam loại II cần 20 g bột cam. Gọi x và y lần lượt là số lít nước cam loại I và II pha chế được. Biết rằng Cúc chỉ có thể dùng không quá 100 g bột cam. Hãy lập các bất phương trình mô tả số lít nước cam loại I và II mà bạn Cúc có thể pha chế được và biểu diễn miền nghiệm của các bất phương trình đó trên cùng một mặt phẳng tọa độ Oxy.

Lời giải:

Vì x, y là là số lít nước cam loại I và II pha chế được nên x ≥ 0 và y ≥ 0.

Số gam bột cam cần dùng để pha chế x lít nước cam loại I là : 30x (g).

Số gam bột cam cần dùng để pha chế y lít nước cam loại II là : 20y (g).

Số gam bột cam Cúc cần dùng để pha hai loại nước cam là : 30x + 20y (g).

Vì số bột cam Cúc có thể dùng không quá 100 g nên ta có bất phương trình : 30x + 20y ≤ 100 hay 3x + 2y ≤ 10.

Vậy ta có ba bất phương trình mô tả số lít nước cam loại I và II mà bạn Cúc có thể pha chế được là:

x ≥ 0;

y ≥ 0;

3x + 2y – 10  ≤  0.

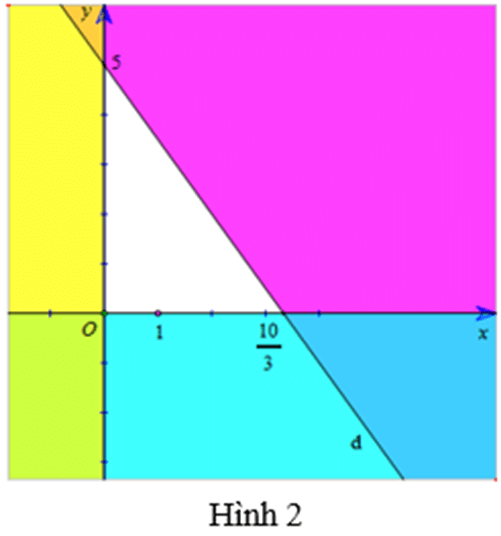
Biểu diễn miền nghiệm của ba bất phương trình trên cùng một mặt phẳng tọa độ Oxy ta được:

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bên phải trục Ox, kể cả bờ Ox, (là miền không tô màu vàng trong hình 2).

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía trên trục Oy, kể cả bờ Oy, (là miền không tô màu xanh trong hình 2).

+ Miền nghiệm của bất phương trình 3x + 2y – 10  ≤  0 là nửa mặt phẳng kể cả bờ d, chứa điểm O (là miền không tô màu tím trong hình 2).

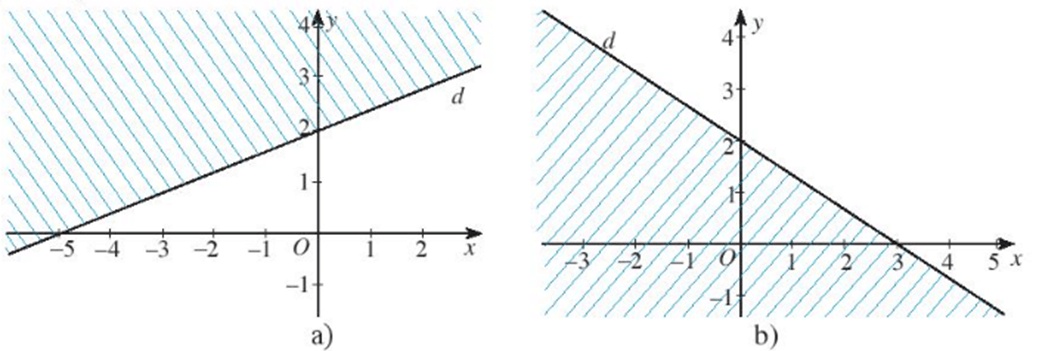
Bài 5 trang 32 Toán lớp 10 Tập 1: Miền không gạch chéo (không kể bờ d) trong mỗi hình dưới đây là miền nghiệm của bất phương trình nào ?

Lời giải:

a) Giả sử phương trình đường thẳng d có dạng là y = ax + b

Đường thẳng d đi qua hai điểm (0; 2) và (- 5; 0) nên ta có:

$\left\{\begin{array}{c}2=a.0+b\\ 0=a.(-5)+b\end{array}\right.$

Giải hệ trên ta được a = $\frac{2}{5}$, b = 2. Suy ra y = $\frac{2}{5}$x + 2 hay 2x – 5y + 10 = 0.

Vậy ta có phương trình đường thẳng d là 2x – 5y + 10 = 0.

Mặt khác O (0; 0) không thuộc d và thuộc miền nghiệm của bất phương trình.

Mà  2.0 – 5.0 + 10 = 10 > 0.

Hơn nữa miền nghiệm không kể đường thẳng d nên bất phương trình cần tìm là 2x – 5y + 10 > 0.

b) Giả sử phương trình đường thẳng d có dạng là y = ax + b

Đường thẳng d đi qua hai điểm (3; 0) và (0; 2) nên ta có:

$\left\{\begin{array}{c}0=a.3+b\\ 2=a.0+b\end{array}\right.$

Giải hệ trên ta được a = $-\frac{2}{3}$ , b = 2. Suy ra y = $-\frac{2}{3}$x + 2 hay 2x + 3y – 6 = 0.

Vậy ta có phương trình đường thẳng d là 2x + 3y – 6 = 0.

Mặt khác O (0; 0) không thuộc d và  không thuộc miền nghiệm của bất phương trình.

Mà 2.0 + 3.0 – 6  = – 6  < 0.

Hơn nữa miền nghiệm của bất phương trình không kể đường thẳng d nên bất phương trình cần tìm là 2x + 3y – 6 > 0.

Lời giải bài tập Toán lớp 10 Bài 1: Bất phương trình bậc nhất hai ẩn Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 29

• Giải Toán 10 trang 30