Giải Toán 10 trang 43 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 43 Tập 1 trong Bài 1: Hàm số và đồ thị Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 43.

Giải Toán 10 trang 43 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 43 Toán lớp 10 Tập 1: Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:

Vì sao bảng này biểu thị một hàm số ? Tìm tập xác định của hàm số này.

Lời giải:

Dựa vào bảng ta thấy, với mỗi một mốc thời gian (t) ta xác định được một và chỉ một giá trị tương ứng của vận tốc (v). Do đó v là hàm số của t.

Tập xác định của hàm số là: D = {0,5; 1; 1,2; 1,8; 2,5}.

Thực hành 2 trang 43 Toán lớp 10 Tập 1: Tìm tập xác định của các hàm số sau:

a) f(x) =  $\sqrt{2x+7}$

b) f(x) = $\frac{x+4}{x^2-3x+2}$

Lời giải:

a)

Biểu thức f(x) có nghĩa nếu và chỉ nếu 2x + 7  0

⇔ 2x ≥ - 7

⇔ x ≥ $-\frac{7}{2}$

Vậy tập xác định của hàm số này là D = $\left[\frac{-7}{2};+\infty \right)$

b)

Biểu thức f(x) có nghĩa nếu và chỉ nếu: $x^2-3x+2\ne 0$

$\iff \left(x-2\right)\left(x-1\right)\ne 0$

$\iff \left\{\begin{array}{l}x-2\ne 0\\ x-1\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}x\ne 2\\ x\ne 1\end{array}\right.$

Vậy tập xác định của hàm số này là D = \{1; 2}.

Vận dụng trang 43 Toán lớp 10 Tập 1: Ở góc của miếng đất hình chữ nhật, người ta làm một bồn hoa có dạng một phần tư hình tròn với bán kính r (Hình 2). Bán kính bồn hoa có kích thước từ 0,5m đến 3m.

a) Viết công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r và tìm tập xác định của hàm số này.

b) Bán kính bồn hoa bằng bao nhiêu thì nó có diện tích là $0,5\pi m^2$  ?

Lời giải:

a) Vì bồn hoa có dạng một phần tư hình tròn nên diện tích bồn hoa là: $S=\frac{\pi r^2}{4}\left(m^2\right)$

Do đó ta được công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r là:

$S=\frac{\pi r^2}{4}$ với 0,5 ≤ r ≤ 3.

Khi đó, tập xác định của hàm số là D = [0,5; 3].

Vậy công thức hàm số biểu thị diện tích bồn hoa theo r là $S=\frac{\pi r^2}{4}$ với D = [0,5; 3].

b) Thay S = 0,5π vào biểu công thức hàm số trên, ta được:

$0,5\pi =\frac{\pi r^2}{4}\iff r^2=2\iff \left[\begin{array}{l}r=\sqrt{2}\\ r=-\sqrt{2}\end{array}\right.$

Mà r ∈ D nên  $r=\sqrt{2}$ (thỏa mãn) và $r=-\sqrt{2}$ (không thỏa mãn).

Vậy với $r=\sqrt{2}$  m thì bồn hoa có diện tích là 0,5π m²_.

Hoạt động khám phá 2 trang 43 Toán lớp 10 Tập 1: Xét hàm số f(x) cho bởi bảng sau:

a) Tìm tập xác định D của hàm số trên.

b) Trong mặt phẳng tọa độ Oxy, vẽ tất cả các điểm có tọa độ (x; y) với x ∈ D và y = f(x).

Lời giải:

a) Từ bảng trên, ta thấy tập xác định D của hàm số là tập tất cả các giá trị của x:

D = {-2; -1; 0; 1; 2; 3; 4}.

b) Từ bảng trên ta có:

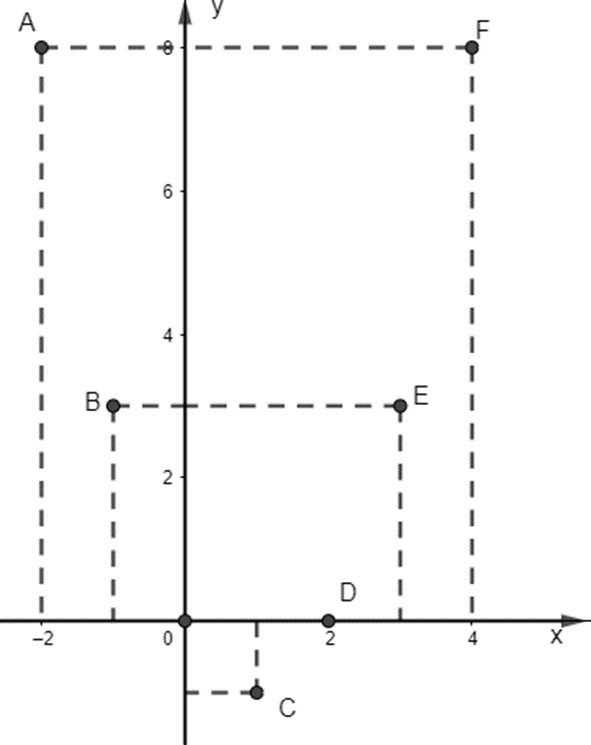
Với x = -2 thì y = f(x) = 8, ta được điểm A(-2; 8).

Với x = -1 thì y = f(x) = 3, ta được điểm B(-1; 3).

Với x = 0 thì y = f(x) = 0, ta được điểm O(0; 0).

Với x = 1 thì y = f(x) = -1, ta được điểm C(1; -1).

Với x = 2 thì y = f(x) = 0, ta được điểm D(2; 0).

Với x = 3 thì y = f(x) = 3, ta được điểm E(3; 3).

Với x = 4 thì y = f(x) = 8, ta được điểm F(4; 8).

Các điểm trên được biểu diễn trên trục tọa độ như sau:

Lời giải bài tập Toán lớp 10 Bài 1: Hàm số và đồ thị Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 41

• Giải Toán 10 trang 44

• Giải Toán 10 trang 45

• Giải Toán 10 trang 47

• Giải Toán 10 trang 48