Xét tính đồng biến, nghịch biến của hàm số y = căn bậc hai của 3x+ 3. A. Hàm số đã cho đồng biến trên tập xác định; B. Hàm số đã cho nghịch biến trên tập xác định; C. Hàm số đã cho vừa đồn
Câu hỏi:
Xét tính đồng biến, nghịch biến của hàm số \(y = \sqrt[3]{x} + 3\).
A. Hàm số đã cho đồng biến trên tập xác định;
B. Hàm số đã cho nghịch biến trên tập xác định;
C. Hàm số đã cho vừa đồng biến, vừa nghịch biến trên tập xác định;
D. Không thể xác định được hàm số đồng biến hay nghịch biến trên tập xác định.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Xét hàm số \(y = f\left( x \right) = \sqrt[3]{x} + 3\).
Tập xác định của hàm số này là D = ℝ.
Lấy x1, x2 tùy ý thuộc ℝ sao cho x1 < x2, ta có: x1 < x2.
Suy ra \(\sqrt[3]{{{x_1}}} < \sqrt[3]{{{x_2}}}\).
Khi đó ta có \(\sqrt[3]{{{x_1}}} + 3 < \sqrt[3]{{{x_2}}} + 3\).
Do đó f(x1) < f(x2).
Vì vậy hàm số đã cho đồng biến (tăng) trên ℝ.
Vậy ta chọn phương án A.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Giá trị m để đồ thị hàm số y = 2x – m + 6 đi qua điểm H(2; –5) là:
Xem lời giải »
Câu 2:
Đồ thị hàm số y = –x2 + 2x + 3 cắt trục hoành tại mấy điểm?
Xem lời giải »
Câu 3:
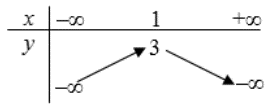
Hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây là:
Xem lời giải »
Câu 4:
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - 2x + 1,\,\,\,\,khi\,\,x \le - 3\\\frac{{x + 7}}{2},\,\,\,\,\,\,\,\,khi\,\,x > - 3\end{array} \right.\). Nếu f(x0) = 5 thì x0 bằng:
Xem lời giải »
Câu 5:
Cho hàm số y = 2x2 – 4x + 3 có đồ thị là parabol (P). Mệnh đề nào sau đây sai?
Xem lời giải »
Câu 6:
Cho hàm số y = –x2 – x – 1. Tập giá trị của hàm số đã cho là:
Xem lời giải »
Câu 8:
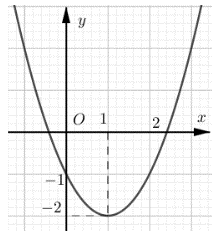
Hàm số y = –x2 + 2x + 3 có đồ thị là hình nào trong các hình sau?
Xem lời giải »