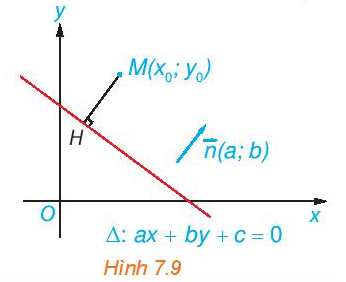
Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến vecto n ( a;b ). Gọi H là hình chiếu vuông góc của M trên ∆ (H.7.9).

Cho điểm M(x₀; y₀) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến \(\overrightarrow n \left( {a;\,b} \right)\). Gọi H là hình chiếu vuông góc của M trên ∆ (H.7.9).

a) Chứng minh rằng \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \sqrt {{a^2} + {b^2}} .HM\).

b) Giả sử H có tọa độ (x₁; y₁). Chứng minh rằng: \(\overrightarrow n .\overrightarrow {HM} \) = a(x₀ – x₁) + b(y₀ – y₁) = ax₀ + by₀ + c.

c) Chứng minh rằng \(HM = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).

Hướng dẫn giải

a) Do H là hình chiếu của M lên ∆ nên MH ⊥ ∆.

Vectơ \(\overrightarrow n \) là vectơ pháp tuyến của ∆ nên giá của vectơ \(\overrightarrow n \) vuông góc với ∆.

Khi đó đường thẳng MH song song hoặc trùng với giá của vectơ \(\overrightarrow n \) nên hai vectơ \(\overrightarrow {HM} \) và \(\overrightarrow n \) cùng phương.

Do đó hai vectơ \(\overrightarrow {HM} \) và \(\overrightarrow n \)cùng hướng hoặc ngược hướng.

+) Nếu hai vectơ \(\overrightarrow {HM} \) và \(\overrightarrow n \)cùng hướng thì \(\overrightarrow n .\overrightarrow {HM} = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {HM} } \right| = \sqrt {{a^2} + {b^2}} .HM\).

+) Nếu hai vectơ \(\overrightarrow {HM} \) và \(\overrightarrow n \)ngược hướng thì \(\overrightarrow n .\overrightarrow {HM} = - \left| {\overrightarrow n } \right|.\left| {\overrightarrow {HM} } \right| = - \sqrt {{a^2} + {b^2}} .HM\).

Vậy \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \sqrt {{a^2} + {b^2}} .HM\).

b) Vì H thuộc ∆ nên tọa độ của H thỏa mãn phương trình ∆, thay tọa độ của H vào phương trình ∆ ta được: ax₁ + by₁ + c = 0 ⇔ c = – ax₁ – by₁      (1).

Ta lại có: \(\overrightarrow {HM} = \left( {{x_0} - {x_1};{y_0} - {y_1}} \right)\).

Suy ra: \(\overrightarrow n .\overrightarrow {HM} = a\left( {{x_0} - {x_1}} \right) + b\left( {{y_0} - {y_1}} \right)\)= ax₀ + by₀ – ax₁ – by₁                  (2).

Từ (1) và (2) suy ra: \(\overrightarrow n .\overrightarrow {HM} = a\left( {{x_0} - {x_1}} \right) + b\left( {{y_0} - {y_1}} \right)\)= ax₀ + by₀ + c.

c) Theo câu a) ta có: \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \sqrt {{a^2} + {b^2}} .HM\).

Theo câu b) ta có: \(\overrightarrow n .\overrightarrow {HM} \) = ax₀ + by₀ + c.

Suy ra: |ax₀ + by₀ + c| = \(\sqrt {{a^2} + {b^2}} .HM\).

Vậy \(HM = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).