Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15 m, chiều rộng AB = 12 m. Phần tam giác DEF là nơi ông bà nuôi vịt,
Câu hỏi:
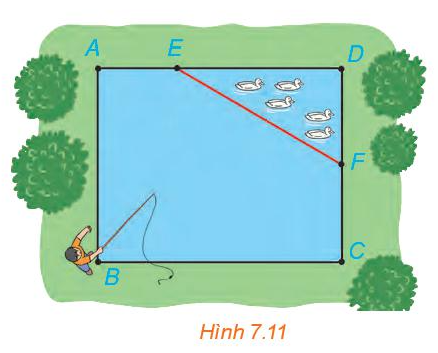
Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15 m, chiều rộng AB = 12 m. Phần tam giác DEF là nơi ông bà nuôi vịt, AE = 5 m, CF = 6 m (H.7.11).
a) Chọn hệ trục tọa độ Oxy, có điểm O trùng với điểm B, các tia Ox, Oy tương ứng trùng với các tia BC, BA. Chọn 1 đơn vị độ dài trên mặt phẳng tọa độ tương ứng với 1 m trong thực tế. Hãy xác định tọa độ của các điểm A, B, C, D, E, F và viết phương trình đường thẳng EF.
b) Nam đứng ở vị trí B câu cá và có thể quăng lưỡi câu xa 10,7 m. Hỏi lưỡi câu có thể rơi vào nơi nuôi vịt hay không ?
Trả lời:
Hướng dẫn giải
a) Đặt hệ trục tọa độ như hình vẽ sau:
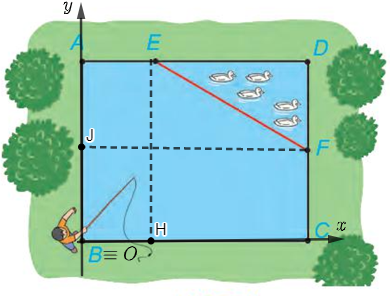
Vì B trùng với gốc tọa độ O nên B có tọa độ là (0; 0).
Vì ABCD là hình chữ nhật nên CD = AB = 12 m, BC = AD = 15 m.
Điểm A thuộc trục Oy và có AO = AB = 12 m nên A có tọa độ là (0; 12).
Điểm C thuộc trục Ox và có CO = CB = 15 m nên C có tọa độ là (15; 0).
Ta có: DC ⊥ Ox (do DC ⊥ BC), DA ⊥ Oy (do DA ⊥ AB) và DC = 12 m, DA = 15 m nên điểm D có tọa độ là (15; 12).
Từ E kẻ EH vuông góc với BC, H thuộc BC nên EH = AB = 12 m, lại có AE = 5 m, do đó điểm E có tọa độ là (5; 12).
Từ F kẻ FJ vuông góc với AB, J thuộc AB nên FJ = AD = 15 m, lại có CF = 6 m, do đó điểm F có tọa độ là (15; 6).
Vậy A(0; 12), B(0; 0), C(15; 0), D(15; 12), E(5; 12), F(15; 6).
Ta có: \[\overrightarrow {EF} = \left( {15 - 5;6 - 12} \right) = \left( {10; - 6} \right)\].
Chọn vectơ \(\overrightarrow u = \frac{1}{2}\overrightarrow {EF} = \left( {5; - 3} \right)\) làm vectơ chỉ phương của đường thẳng EF thì vectơ pháp tuyến của đường thẳng EF là \(\overrightarrow n = \left( {3;\,5} \right)\).
Đường thẳng EF đi qua điểm E(5; 12) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {3;\,5} \right)\), do đó phương trình đường thẳng EF là: 3(x – 5) + 5(y – 12) = 0 hay 3x + 5y – 75 = 0.
b) Áp dụng công thức tính khoảng cách, ta có khoảng cách từ B đến EF là:
\(d\left( {B,\,EF} \right) = \frac{{\left| {3.0 + 5.0 - 75} \right|}}{{\sqrt {{3^2} + {5^2}} }} = \frac{{75}}{{\sqrt {34} }}\)≈ 12,9 m.
Khoảng cách từ B đến EF là đường ngắn nhất từ B nơi Nam đứng đến EF, lưỡi câu có thể quăng xa 10,7 m và 10,7 m < 12,9 m nên lưỡi câu không thể rơi vào vị trí nuôi vịt.