Cho đường tròn (C) có phương trình x2 + y2 – 4x + 6y – 12 = 0. a) Tìm tọa độ tâm I và bán kính R của (C). b) Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) t
Câu hỏi:
Cho đường tròn (C) có phương trình x2 + y2 – 4x + 6y – 12 = 0.
a) Tìm tọa độ tâm I và bán kính R của (C).
b) Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) tại M.
Trả lời:
Hướng dẫn giải
a) Ta có: x2 + y2 – 4x + 6y – 12 = 0 ⇔ x2 + y2 – 2 . 2 . x – 2 . (– 3) . y – 12 = 0.
Có các hệ số: a = 2, b = – 3, c = – 12.
Do đó, đường tròn (C) có tâm I(2; – 3) và bán kính R = \(\sqrt {{2^2} + {{\left( { - 3} \right)}^2} - \left( { - 12} \right)} = \sqrt {25} = 5\).
b) Vì 52 + 12 – 4 . 5 + 6 . 1 – 12 = 0 nên điểm M(5; 1) thuộc (C).
Tiếp tuyến d của (C) tại M có vectơ pháp tuyến là \(\overrightarrow {IM} = \left( {5 - 2;1 - \left( { - 3} \right)} \right) = \left( {3;4} \right)\) và đi qua M(5; 1) nên có phương trình là: 3(x – 5) + 4(y – 1) = 0 hay 3x + 4y – 19 = 0.
Xem thêm lời giải bài tập Toán 10 Kết nối tri thức hay, chi tiết:
Câu 1:
A – Trắc nghiệm
Phương trình nào sau đây là phương trình tham số của đường thẳng?
Xem lời giải »
Câu 2:
Phương trình nào sau đây là phương trình tổng quát của đường thẳng?
Xem lời giải »
Câu 3:
Phương trình nào sau đây là phương trình của đường tròn?
Xem lời giải »
Câu 4:
Phương trình nào sau đây là phương trình chính tắc của đường elip?
Xem lời giải »
Câu 5:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,\,\left( {a > b > 0} \right)\).
a) Tìm các giao điểm A1, A2 của (E) với trục hoành và các giao điểm B1, B2 của (E) với trục tung. Tính A1A2, B1B2.
b) Xét một điểm bất kì M(x0; y0) thuộc (E).
Chứng minh rằng, b2 ≤ x02 + y02 ≤ a2 và b ≤ OM ≤ a.
Chú ý: A1A2, B1B2 tương ứng được gọi là trục lớn, trục nhỏ của elip (E) và tương ứng có độ dài là 2a, 2b.
Xem lời giải »
Câu 6:
Cho hypebol có phương trình: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
a) Tìm các giao điểm A1, A2 của hypebol với trục hoành (hoành độ của A1 nhỏ hơn của A2).
b) Chứng minh rằng, nếu điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì x ≤ − a, nếu điểm M(x; y) thuộc nhánh nằm bên phải trục tung của hypebol thì x ≥ a.
c) Tìm các điểm M1, M2 tương ứng thuộc cách nhánh bên trái, bên phải trục tung của hypebol để M1M2 nhỏ nhất.
Xem lời giải »
Câu 7:
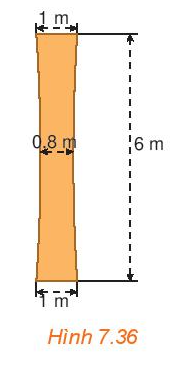
Một cột trụ hình hypebol (H.7.36), có chiều cao 6 m, chỗ nhỏ nhất ở chính giữa và rộng 0,8 m, đỉnh cột và đáy cột đều rộng 1 m. Tính độ rộng của cột ở độ cao 5 m (tính theo đơn vị mét và làm tròn tới hai chữ số sau dấu phẩy).
Xem lời giải »