Cho f(x) = x^2 – 1. Tìm khẳng định sai trong các khẳng định sau
Câu hỏi:
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
A. f(x) < 0 khi x ∈ (– 1; 1);
B. f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞)
C. f(x) = 0 khi x = 1; x = – 1;
D. f(x) > 0 khi x ∈ (– 1; 1);
Trả lời:
Đáp án đúng là: D
Xét f(x) = x2 – 1 có ∆ = – 4.(–1) = 4 > 0, a = 1 > 0 và có hai nghiệm phân biệt x1 = –1 và x2 = 1.
Khi đó ta có bảng xét dấu:
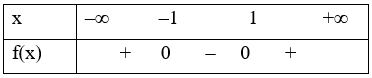
Từ bảng xét dấu ta có f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞); f(x) < 0 khi x ∈ (– 1; 1)
Vậy khẳng định sai là D

