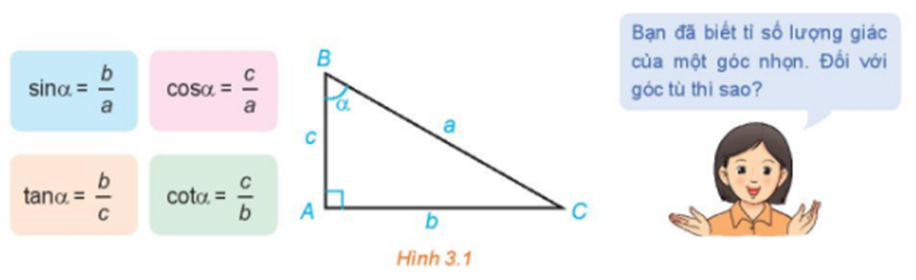
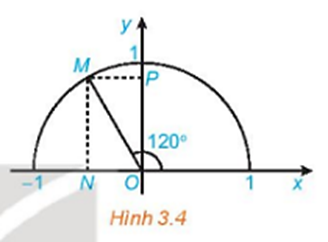
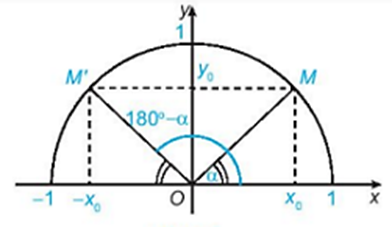
Cho góc alpha (0 độ < alpha < 180 độ) thỏa mãn tan alpha = 3. TÍnh giá trị của biểu thức P

Câu hỏi:

Trả lời:

Ta có: $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }$  (α ≠ 90^o)

$\Rightarrow \frac{1}{{\cos }^2\alpha }=1+3^2=10$

$\Rightarrow {\cos }^2\alpha =\frac{1}{10}\iff \cos \alpha =\pm \frac{\sqrt{10}}{10}$

Vì 0^o < α < 180^o nên sin α > 0.

Mà tan α = 3 > 0 Þ cos α > 0 Þ $\cos \alpha =\frac{\sqrt{10}}{10}$ .

Lại có: sin α = cos α . tan α = $3.\frac{\sqrt{10}}{10}=\frac{3\sqrt{10}}{10}$ .

Do đó $P=\frac{2\sin \alpha -3\cos \alpha }{3\sin \alpha +2\cos \alpha }=\frac{2.\frac{3\sqrt{10}}{10}-3.\frac{\sqrt{10}}{10}}{3.\frac{3\sqrt{10}}{10}+2.\frac{\sqrt{10}}{10}}$

$=\frac{\frac{\sqrt{10}}{10}(2.3-3)}{\frac{\sqrt{10}}{10}(3.3+2)}=\frac{3}{11}$

Vậy với α (0^o < α < 180^o) thỏa mãn tan α = 3 thì .