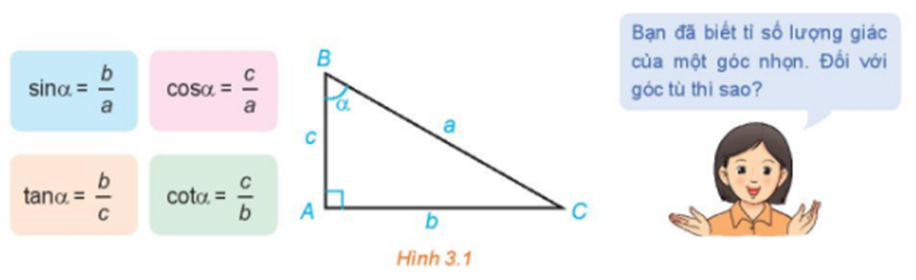
a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi
Câu hỏi:
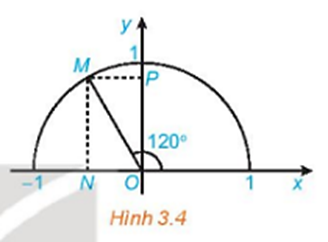
a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
b) Khi , nêu mối quan hệ giữa với hoành độ và tung độ của điểm M.
Trả lời:
a)
Gọi điểm A có tọa độ A(1; 0).
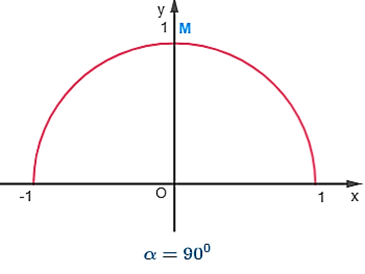
• α = 90o hay . Khi đó, điểm M có tọa độ M(0; 1).
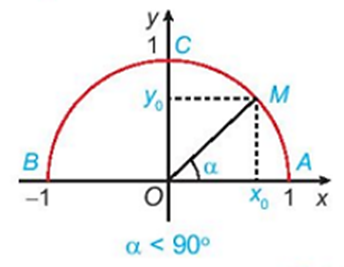
Do đó, điểm M(x0; y0) nằm trên cung tròn (không tính điểm C) thỏa mãn 0 < x0 ≤ 1, 0 ≤ y0 < 1.
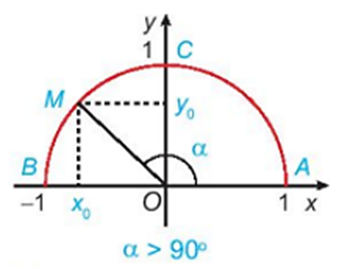
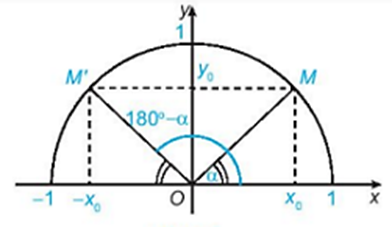
• α > 90o hay .
Do đó, điểm M(x0; y0) nằm trên cung tròn (không tính điểm C) thỏa mãn −1 ≤ x0 < 0, 0 ≤ y0 < 1.
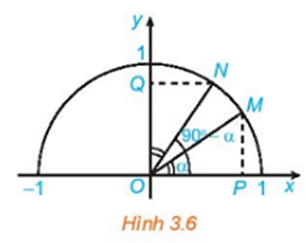
b) Khi 0o < α < 90o
Kẻ MH ^ Ox, MK ^ Oy (H Î Ox, H Î Oy). Khi đó .
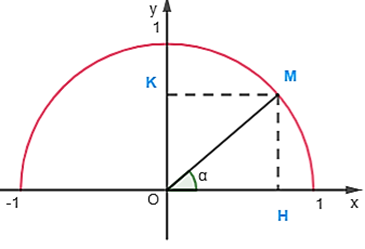
Gọi điểm M có tọa độ M(x0; y0).
Xét tứ giác MKOH có:
(Ox ^ Oy)
(MH ^ Ox)
(MK ^ Oy)
Do đó tứ giác MKOH là hình chữ nhật.
Suy ra OH = |x0| = x0; MH = OK = |y0| = y0.
Ta có OM = 1 (bán kính đường tròn đơn vị).
Xét ∆MHO vuông tại H, ta có:
.
Hay sin α = y0.
Ta lại có: .
Hay cos α = x0.
Vậy cos α là hoành độ của điểm M và sin α là tung độ của điểm M.