Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau. Các số đo độ phân tán
Câu hỏi:
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau. Các số đo độ phân tán (khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn) sẽ thay đổi như thế nào nếu:
a) Nhân mỗi giá trị của mẫu số liệu với 2.
b) Cộng mỗi giá trị của mẫu số liệu với 2.
Trả lời:
Lời giải:
a) Gọi các giá trị dương của mẫu số liệu ban đầu theo thứ tự không giảm là:
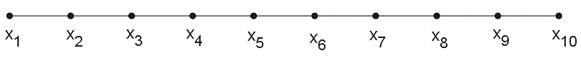
Ta có n = 10 là số chẵn nên trung vị là giá trị trung bình của số thứ 5 và thứ 6.
Do đó Q1 là số thứ 3 và Q3 là số thứ 8.
a) Khi nhân mỗi giá trị của mẫu số liệu với 2 thì
+ Số lớn nhất tăng 2 lần và số nhỏ nhất tăng 2 lần nên khoảng biến thiên R tăng 2 lần.
+ Q1 và Q3 tăng 2 lần nên khoảng tứ phân vị ΔQ = Q3 − Q1 tăng 2 lần.
+ Giá trị trung bình tăng 2 lần.
Nên độ lệch của mỗi giá trị so với giá trị trung bình cũng tăng 2 lần.
Suy ra tăng 4 lần.
Khi đó, phương sai tăng 4 lần.
Do đó độ lệch chuẩn tăng 2 lần.
Vậy các khoảng biến thiên, độ lệch chuẩn, khoảng tứ phân vị của dãy số liệu mới bằng hai lần các khoảng biến thiên, độ lệch chuẩn, khoảng tứ phân vị ban đầu.
b) Khi cộng mỗi giá trị của mẫu số liệu với 2 thì
+ Số lớn nhất tăng 2 đơn vị và số nhỏ nhất tăng 2 đơn vị.
Suy ra khoảng biến thiên R không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ Q1 và Q3 tăng 2 đơn vị nên khoảng tứ phân vị ΔQ = Q3 − Q1 không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ Giá trị trung bình tăng 2 đơn vị
Nên độ lệch của mỗi giá trị so với giá trị trung bình không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
Suy ra không đổi
Khi đó, phương sai không đổi.
Do đó độ lệch chuẩn không đổi.
Vậy khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn đều không đổi.

