Cho tam giác ABC . Lấy E là trung điểm của AB và F thuộc cạnh AC
Câu hỏi:
Cho tam giác ABC . Lấy E là trung điểm của AB và F thuộc cạnh AC sao cho AF = \[\frac{1}{3}\]AC. Hãy xác định điểm M để \(\overrightarrow {MA} + 3\overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).
A. M là trung điểm BC;
B. M là đỉnh hình chữ nhật AEFM;
C. M là đỉnh hình bình hành EAFM;
D. M là đỉnh tam giác đều BEM.
Trả lời:
Đáp án đúng là C
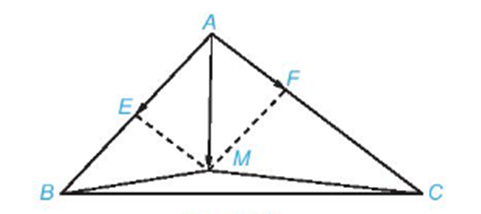
Để xác định vị trí điểm M, trước hết ta biểu thị \(\overrightarrow {AM} \) (với gốc A đã biết) theo hai vec tơ \(\overrightarrow {AB} ,\overrightarrow {AC} \).
Đẳng thức vec tơ đã cho tương đương với \(\overrightarrow {MA} + 3\left( {\overrightarrow {MA} + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA} + \overrightarrow {AC} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 6\overrightarrow {MA} + 3\overrightarrow {AB} + 2\overrightarrow {AC} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
Vì E là trung điểm của AB và F thuộc cạnh AC sao cho AF = \[\frac{1}{3}\]AC nên \(\overrightarrow {AE} = \frac{1}{2}\overrightarrow {AB} \) và \(\overrightarrow {AF} = \frac{1}{3}\overrightarrow {AC} \).
Vì vậy \(\overrightarrow {AM} = \overrightarrow {AE} + \overrightarrow {AF} \).
Suy ra M là đỉnh thứ tư của hình bình hành EAFM.