Tam giác ABC có AC = 3 căn bậc hai 3, AB = 3, BC = 6
Câu hỏi:
Tam giác ABC có \(AC = 3\sqrt 3 \), AB = 3, BC = 6. Tính số đo góc B
Trả lời:
Đáp án đúng là: A
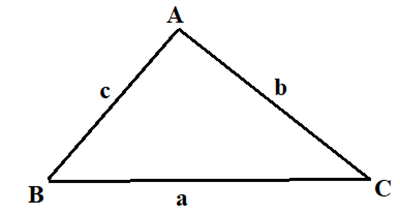
Áp dụng hệ quả của định lý côsin, ta có: \[\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\]
\[ \Leftrightarrow \cos B = \frac{{B{C^2} + A{B^2} - A{C^2}}}{{2AB.BC}} = \frac{{{6^2} + {3^2} - {{\left( {3\sqrt 3 } \right)}^2}}}{{2.6.3}} = \frac{1}{2} \Rightarrow \widehat B = 60^\circ \].
Xem thêm bài tập trắc nghiệm Toán 10 KNTT có lời giải hay khác:
Câu 1:
Tam giác ABC có A = 120° khẳng định nào sau đây đúng?
Xem lời giải »
Câu 3:
Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.
Xem lời giải »
Câu 5:
Tam giác ABC có tổng hai góc B và C bằng 135° và độ dài cạnh BC bằng a. Tính bán kính đường tròn ngoại tiếp tam giác.
Xem lời giải »
Câu 6:
Kết quả rút gọn của biểu thức \(A = \frac{{\cos ( - 108^\circ ).\cot 72^\circ }}{{\tan ( - 162^\circ ).\sin 108^\circ }} - \tan 18^\circ \) là :
Xem lời giải »
Câu 7:
Rút gọn biểu thức \(A = \frac{{{{(1 - {{\tan }^2}\alpha )}^2}}}{{4{{\tan }^2}\alpha }} - \frac{1}{{4{{\sin }^2}\alpha .co{s^2}\alpha }}\) bằng:
Xem lời giải »
Câu 8:
Biểu thức A = cos2α.cot2α + 3cos2α – cot2α + 2sin2 α bằng.
Xem lời giải »

