Tập ngiệm của bất phương trình: x(x + 5) < = 2(x^2 + 2) là:
Câu hỏi:
Tập ngiệm của bất phương trình: x(x + 5) ≤ 2(x2 + 2) là:
A. \[(--\infty ;1] \cup [4; + \infty )\] ;
B. \(\left[ {1;4} \right]\) ;
C. \[(--\infty ;1) \cup (4; + \infty )\];
D. \((1;4)\).
Trả lời:
Đáp án đúng: A
Ta có: x(x + 5) ≤ 2(x2 + 2) \( \Leftrightarrow \)x2 – 5x + 4 ≥ 0
Đặt f(x) = x2 – 5x + 4 ta có f(x) = 0 \( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\).
Ta có bảng xét dấu :
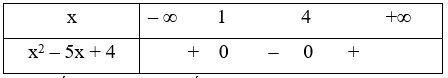
Dựa vào bảng xét dấu nghiệm của bất phương trình \[x \in (--\infty ;1] \cup [4; + \infty )\]