Câu hỏi:
B. Bài tập
Tìm tâm và bán kính của đường tròn (x + 3)2 + (y – 3)2 = 36.
Trả lời:
Hướng dẫn giải
Ta viết phương trình đường tròn đã cho về dạng: (x – (– 3))2 + (y – 3)2 = 62.
Do đó đường tròn này có tâm I(– 3; 3) và bán kính R = 6.
Câu 1:
A. Các câu hỏi trong bài
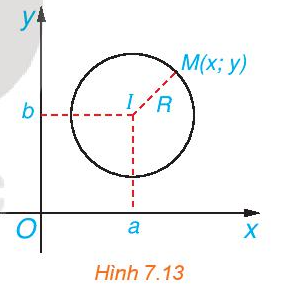
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C), tâm I(a; b), bán kính R (H.7.13). Khi đó, một điểm M(x; y) thuộc đường tròn (C) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện đại số nào?
Câu 3:
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn. Tìm tâm và bán kính của đường tròn đó.
a) x2 – y2 – 2x + 4y – 1 = 0;
b) x2 + y2 – 2x + 4y + 6 = 0;
c) x2 + y2 + 6x – 4y + 2 = 0.
Câu 4:
Câu 5:
a) x2 + y2 + xy + 4x – 2 = 0;
b) x2 + y2 – 2x – 4y + 5 = 0;
c) x2 + y2 + 6x – 8y + 1 = 0.
Câu 6:
Viết phương trình của đường tròn trong mỗi trường hợp sau:
a) Có tâm I(– 2; 5) và bán kính R = 7;
b) Có tâm I(1; – 2) và đi qua điểm A(– 2; 2);
c) Có đường kính AB, với A(– 1; – 3), B(– 3; 5);
d) Có tâm I(1; 3) và tiếp xúc với đường thẳng x + 2y + 3 = 0.
Câu 7:
Câu 8:
