Giải Toán 10 trang 39 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 39 Tập 1 trong Bài 6: Hệ thức lượng trong tam giác Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 39.

Giải Toán 10 trang 39 Tập 1 Kết nối tri thức

Khám phá trang 39 Toán 10 Tập 1: Từ định lý côsin hãy viết các công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC.

Lời giải:

Từ định lý cosin, ta có công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC là:

$\cos A=\frac{b^2+c^2-a^2}{2bc};$

$\cos B=\frac{a^2+c^2-b^2}{2ac};$

$\cos C=\frac{a^2+b^2-c^2}{2ab}.$

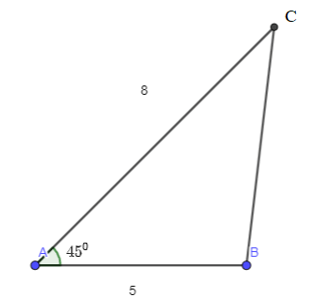
Luyện tập 1 trang 39 Toán 10 Tập 1: Cho tam giác ABC, có AB = 5, AC = 8 và $\widehat{A}=45°$. Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.

Lời giải:

Xét tam giác ABC:

Theo định lí côsin, ta có:

BC² = AB² + AC² – 2.AB.AC.cos A

BC² = 5² + 8² – 2.5.8.cos45°

BC² = $89-40\sqrt{2}$

BC ≈ 5,7 cm.

Ta có:

$\text{cos}C=\frac{B{C}^2+A{C}^2-A{B}^2}{2.BC.AC}=\frac{{\left(5,7\right)}^2+8^2-5^2}{2.5,7.8}\approx 0,7839 \Rightarrow C\approx 38°23\text{'}$

$\text{cosB}=\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{5^2+{\left(5,7\right)}^2-8^2}{\mathrm{2.5.5},7}\approx -0,1153 \Rightarrow B\approx 96°37\text{'}$

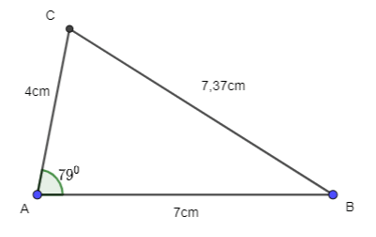
Trải nghiệm trang 39 Toán 10 Tập 1: Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số đo góc A và kiểm tra tính đúng đắn của Định lí Côsin tại đỉnh A đối với tam giác đó.

Lời giải:

Tiến hành đo các cạnh của tam giác và góc A, ta được:

AB = 7cm, AC = 4cm, BC = 7,37cm và $\widehat{A}=79°$.

Khi đó, ta có:

$\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{7^2+4^2-7,{37}^2}{\mathrm{2.7.4}}$ ≈ 0,19.

cosA = cos79⁰ ≈ 0,19.

Do đó $\text{cos}A=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}$.

Vì vậy Định lý côsin là đúng.

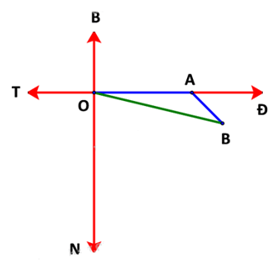
Vận dụng 1 trang 39 Toán 10 Tập 1: Dùng định lí Côsin, tính khoảng cách được đề cập trong HĐ1b.

Lời giải:

Vị trí O là vị trí là vị trí cảng Vân Phong.

Sau khi đi 1 giờ theo hướng đông với vận tốc 20km/h thì tàu đi đến vị trí A, quãng đường OA là: 20.1 = 20 (km)

Đi tiếp 0,5 giờ còn lại theo hướng đông nam cũng với vận tốc 20km/h thì tàu đến vị trí B, quãng đường AB là: 20.0,5 = 10 (km)

Vì hướng đông và hướng đông nam tạo với nhau một góc 45⁰ nên $\widehat{OAB}=135°$.

Xét ΔABC, có:

Theo Định lí Côsin, ta có:

OB² = OA² + AB² – 2.OA.AB.cosA

       = 20² + 10² – 2.20.10.cos135⁰

      = 500 + 200√2

OB ≈ 27,98 km

Vậy sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng vân phong 27,98 km.

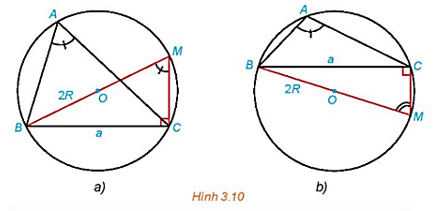
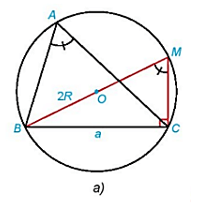
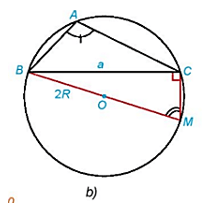
HĐ3 trang 39 Toán 10 Tập 1: Trong mỗi hình dưới đây, hãy tính R theo a và sin A.

Lời giải:

Hình 3.10a):

Xét ΔBCM vuông tại C, có:

$\sin \widehat{BMC}=\frac{BC}{BM}=\frac{a}{2R}$

Mà $\widehat{BMC}+\widehat{A}=180°$ (tứ giác ABMC nối tiếp đường tròn (O)).

$\Rightarrow \widehat{A}=180°-\widehat{BMC}$

$\Rightarrow \sin A=\sin \left(180°-\widehat{BMC}\right)=\sin \widehat{BMC}=\frac{a}{2R}$

$\Rightarrow R=\frac{a}{2\sin A}.$

Hình 3.10b):

Xét ΔBCM vuông tại C, có:

$\sin \widehat{BMC}=\frac{BC}{BM}=\frac{a}{2R}$

Mà

 $\widehat{BMC}+\widehat{A}=\frac{1}{2}sđ\stackrel{⏜}{BAC}+\frac{1}{2}sđ\stackrel{⏜}{BMC}$

$=\frac{1}{2}{.360}^0={180}^0\Rightarrow \widehat{BMC}={180}^0-\widehat{A}$

$\Rightarrow \sin A=\sin \left({180}^0-\widehat{BMC}\right)=\sin \widehat{BMC}=\frac{a}{2R}$

$\Rightarrow R=\frac{a}{2\sin A}.$

Lời giải bài tập Toán lớp 10 Bài 6: Hệ thức lượng trong tam giác Kết nối tri thức hay khác:

• Giải Toán 10 trang 38
• Giải Toán 10 trang 40
• Giải Toán 10 trang 41
• Giải Toán 10 trang 42
• Giải Toán 10 trang 43