Giải Toán 10 trang 41 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 41 Tập 1 trong Bài 6: Hệ thức lượng trong tam giác Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 41.

Giải Toán 10 trang 41 Tập 1 Kết nối tri thức

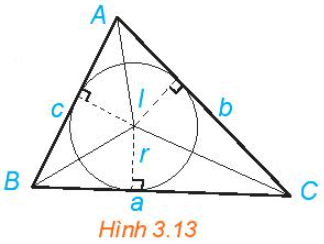
HĐ4 trang 41 Toán 10 Tập 1: Cho ΔABC với I là tâm đường tròn nội tiếp tam giác.

a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích tam giác IBC, ICA, IAB.

b) Tính diện tích tam giác ABC theo r, a, b, c.

Lời giải:

a) Ta có diện tích tam giác ABC bằng tổng diện tích tam giác IAB, IAC, IBC: S_∆ABC = S_∆IBC + S_∆ICA + S_∆IAB

b) Ta có:

$S_{\Delta IBC}=\frac{1}{2}a.r$

$S_{\Delta ICA}=\frac{1}{2}b.r$

$S_{\Delta IAB}=\frac{1}{2}cr$

$\Rightarrow S_{\Delta ABC}=S_{\Delta IBC}+S_{\Delta ICA}+S_{\Delta IAB}$

$=\frac{1}{2}a.r+\frac{1}{2}b.r+\frac{1}{2}c.r=\frac{\left(a+b+c\right).r}{2}.$

Vậy $S_{\Delta ABC}=\frac{\left(a+b+c\right).r}{2}.$

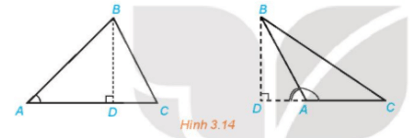
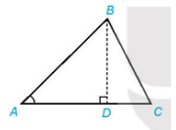
HĐ5 trang 41 Toán 10 Tập 1: Cho tam giác ABC với đường cao BD

a) Biểu thị BD theo AB và sin A.

b) Viết công thức tính diện tích S của tam giác ABC theo b, c, sin A.

Lời giải:

3

a)

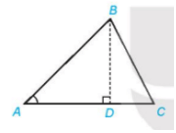
TH1: Đường cao BD nằm trong tam giác ABC

 Xét ΔABD vuông tại D, có:

BD = sinA.AB

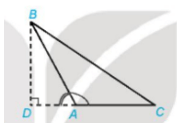
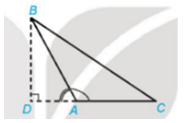
TH2: Đường cao BD nằm ngoài tam giác ABC

Xét ΔABD vuông tại D, có:

$BD=\sin \widehat{BAD}.AB$

Mà $\widehat{BAD}+\widehat{BAC}={180}^0$

$\Rightarrow \sin \widehat{BAC}=\sin \left({180}^0-\widehat{BAD}\right)=\sin \widehat{BAD}$

$\Rightarrow BD=\sin \widehat{BAC}.AB=\sin A.AB$

Vậy trong cả hai trường hợp ta đều có BD = sinA.AB.

b) TH1. Đường cao BD nằm trong tam giác ABC:

$$\begin{gathered} S_{\Delta ABC}=\frac{1}{2}AC.BD=\frac{1}{2}AC.AB.\sin A \\ =\frac{1}{2}.b.c\sin A. \end{gathered}$$

TH2. Đường cao BD nằm ngoài tam giác ABC:

$$\begin{gathered} S_{\Delta ABC}=\frac{1}{2}AC.BD=\frac{1}{2}AC.AB.\sin A \\ =\frac{1}{2}.b.c\sin A. \end{gathered}$$

Vậy cả hai trường hợp $S_{\Delta ABC}=\frac{1}{2}.b.c\sin A.$

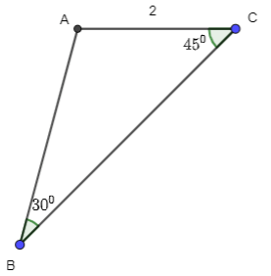
Luyện tập 4 trang 41 Toán 10 Tập 1: Tính diện tích tam giác ABC có b = 2, $\widehat{B}={30}^0,\widehat{C}={45}^0$.

Lời giải:

Xét ΔABC, có:

Theo định lí sin, ta có:

$$\begin{gathered} \frac{AC}{\sin B}=\frac{AB}{\sin C}\iff \frac{2}{\sin {30}^0}=\frac{AB}{\sin {45}^0} \\ \iff AB=\frac{2.\sin {45}^0}{\sin {30}^0}=2\sqrt{2}. \end{gathered}$$

Ta có:

$\widehat{A}={180}^0-\widehat{B}-\widehat{C}$ = 180⁰ – 30⁰ – 45⁰ = 105⁰

Diện tích tam giác ABC là:

$S_{\Delta ABC}=\frac{1}{2}.AB.AC.\sin A$

$=\frac{1}{2}.2\sqrt{2}\mathrm{.2.}\sin {105}^0=1+\sqrt{3}$(đvdt)

Vậy diện tích tam giác ABC là $1+\sqrt{3}$ đvdt.

Thảo luận trang 41 Toán 10 Tập 1: Ta đã biết tính cosA theo độ dài các cạnh của tam giác ABC. Liệu sinA và diện tích S có tính được theo độ dài cạnh của tam giác ABC không?

Lời giải:

sinA và S được tính theo độ dài cạnh của tam giác ABC như sau:

Ta có: $\cos A=\frac{b^2+c^2-a^2}{2bc}$ (định lí côsin)

Ta lại có: cos²A + sin²A = 1  

⇔ sin²A = 1 – cos²A

$\iff {\sin }^{2}A=1-{\left(\frac{b^2+c^2-a^2}{2bc}\right)}^2$

=> $\iff \sin A=\sqrt{\frac{4b^2{c}^2-{\left(b^2+c^2-a^2\right)}^2}{4b^2{c}^2}}$

Khi đó diện tích tam giác ABC là:

$S_{\Delta ABC}=\frac{1}{2}.AB.AC.\sin A=\frac{1}{2}.b.c.\sqrt{\frac{4b^2{c}^2-{\left(b^2+c^2-a^2\right)}^2}{4b^2{c}^2}}$

$=\frac{1}{4}\sqrt{\left(2bc-b^2-c^2+a^2\right)\left(2bc+b^2+c^2-a^2\right)}$

$=\frac{1}{4}\sqrt{\left[a^2-{\left(b-c\right)}^2\right]\left[{\left(b+c\right)}^2-a^2\right]}$

$=\frac{1}{4}\sqrt{\left(a-b+c\right)\left(a+b-c\right)\left(b+c-a\right)\left(b+c+a\right)}$

Lời giải bài tập Toán lớp 10 Bài 6: Hệ thức lượng trong tam giác Kết nối tri thức hay khác:

• Giải Toán 10 trang 38
• Giải Toán 10 trang 39
• Giải Toán 10 trang 40
• Giải Toán 10 trang 42
• Giải Toán 10 trang 43