Giải Toán 10 trang 46 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 46 Tập 2 trong Bài 21: Đường tròn trong mặt phẳng tọa độ Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 46.

Giải Toán 10 trang 46 Tập 2 Kết nối tri thức

HĐ2 trang 46 Toán 10 Tập 2: Cho đường tròn (C): (x – 1)²+ (y – 2)² = 25 và điểm M(4; – 2).

a) Chứng minh điểm M(4; – 2) thuộc đường tròn (C). 

b) Xác định tâm và bán kính của (C).

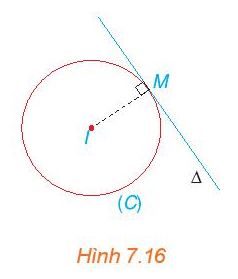
c) Gọi ∆ là tiếp tuyến của (C) tại M. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆ (H.7.16). Từ đó, viết phương trình đường thẳng ∆.

Lời giải:

a) Thay tọa độ điểm M(4; – 2) vào phương trình đường tròn (C) ta được: 

(4 – 1)² + (– 2 – 2)² = 25 ⇔ 3² + (– 4)² = 25 ⇔ 25 = 25 (luôn đúng). 

Vậy điểm M(4; – 2) thuộc đường tròn (C). 

b) Đường tròn (C) có tâm I(1; 2) và bán kính R = $\sqrt{25}$ = 5. 

c) Ta có: ∆ ⊥ IM tại M (bán kính đi qua tiếp điểm thì vuông góc với tiếp tuyến tại tiếp điểm đó). 

Do đó một vectơ pháp tuyến của đường thẳng ∆ là vectơ $\overrightarrow{IM}=\left(4-1;-2-2\right)=\left(3;-4\right)$.

Đường thẳng ∆ đi qua điểm M(4; – 2) và có một vectơ pháp tuyến $\overrightarrow{IM}=\left(3;-4\right)$ nên phương trình đường thẳng ∆ là: 3(x – 4) – 4(y + 2) = 0 hay 3x – 4y – 20 = 0. 

Luyện tập 4 trang 46 Toán 10 Tập 2: Cho đường tròn (C): x² + y² – 2x + 4y + 1 = 0. Viết phương trình tiếp tuyến ∆ của (C) tại điểm N(1; 0). 

Lời giải:

Ta có: x² + y² – 2x + 4y + 1 = 0 ⇔ x² + y² – 2 . 1 . x – 2 . (– 2) . y + 1 = 0 

Các hệ số: a = 1, b = – 2, c = 1. 

Khi đó đường tròn (C) có tâm I(1; – 2). 

Do 1² + 0 – 2 . 1 + 0 + 1 = 0 nên điểm N(1; 0) thuộc (C). 

Tiếp tuyến ∆ của (C) tại điểm N(1; 0) có vectơ pháp tuyến $\overrightarrow{IN}=\left(1-1;0-\left(-2\right)\right)=\left(0;2\right)$, nên có phương trình ∆: 0(x – 1) + 2(y – 0) = 0 hay ∆: y = 0. 

Vận dụng 2 trang 46 Toán 10 Tập 2: Trên mặt phẳng tọa độ Oxy, một vật chuyển động nhanh trên đường tròn có phương trình x² + y² = 25. Khi tới vị trí M(3; 4) thì vật bị văng khỏi quỹ đạo tròn và ngày sau đó, trong một khoảng thời gian ngắn bay theo hướng tiếp tuyến của đường tròn. Hỏi trong khoảng thời gian ngắn ngay sau khi văng, vật chuyển động trên đường thẳng nào ?

Lời giải:

Trong khoảng thời gian ngắn sau khi văng tại vị trí M(3; 4), vật chuyển động trên đường thẳng là tiếp tuyến của đường tròn có phương trình x² + y² = 25 tại điểm M(3; 4). 

Đường tròn (C): x² + y² = 25 có tâm O(0; 0), điểm M(3; 4) thuộc đường tròn đó (vì 3² + 4² = 25). 

Tiếp tuyến của (C) tại M(3; 4) có vectơ pháp tuyến là $\overrightarrow{OM}=\left(3-0;4-0\right)=\left(3;4\right)$, nên có phương trình: 3(x – 3) + 4(y – 4) = 0 hay 3x + 4y – 25 = 0. 

Vậy vật chuyển động trên đường thẳng có phương trình 3x + 4y – 25 = 0 trong khoảng thời gian ngắn ngay sau khi văng. 

Bài 7.13 trang 47 Toán 10 Tập 2: Tìm tâm và bán kính của đường tròn

(x + 3)² + (y – 3)² = 36. 

Lời giải:

Ta viết phương trình đường tròn đã cho về dạng: (x – (– 3))² + (y – 3)² = 6². 

Do đó đường tròn này có tâm I(– 3; 3) và bán kính R = 6. 

Bài 7.14 trang 47 Toán 10 Tập 2: Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng. 

a) x² + y² + xy + 4x – 2 = 0; 

b) x² + y² – 2x – 4y + 5 = 0; 

c) x² + y² + 6x – 8y + 1 = 0. 

Lời giải:

a) Phương trình x² + y² + xy + 4x – 2 = 0 không có dạng x² + y² – 2ax – 2by + c = 0 với a, b, c là các số thực nên đây không phải phương trình đường tròn. 

b) x² + y² – 2x – 4y + 5 = 0 ⇔ x² + y² – 2 . 1 . x – 2 . 2 . y + 5 = 0.

Các hệ số: a = 1, b = 2, c = 5. 

Ta có: a² + b² – c = 1² + 2² – 5 = 0 nên đây cũng không phải phương trình đường tròn. 

c) x² + y² + 6x – 8y + 1 = 0 ⇔ x² + y² – 2 . (– 3) . x – 2 . 4 . y + 1 = 0.

Các hệ số: a = – 3, b = 4, c = 1. 

Ta có: a² + b² – c = (– 3)² + 4² – 1 = 24 > 0 nên đây là phương trình đường tròn. 

Đường tròn này có tâm I(– 3; 4) và bán kính R =$\sqrt{24}$ = $2\sqrt{6}$

Lời giải bài tập Toán lớp 10 Bài 21: Đường tròn trong mặt phẳng tọa độ Kết nối tri thức hay khác:

• Giải Toán 10 trang 43

• Giải Toán 10 trang 44

• Giải Toán 10 trang 45

• Giải Toán 10 trang 47