Giải Toán 10 trang 47 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 47 Tập 2 trong Bài 21: Đường tròn trong mặt phẳng tọa độ Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 47.

Giải Toán 10 trang 47 Tập 2 Kết nối tri thức

Bài 7.15 trang 47 Toán 10 Tập 2: Viết phương trình của đường tròn trong mỗi trường hợp sau: 

a) Có tâm I(– 2; 5) và bán kính R = 7; 

b) Có tâm I(1; – 2) và đi qua điểm A(– 2; 2);

c) Có đường kính AB, với A(– 1; – 3), B(– 3; 5); 

d) Có tâm I(1; 3) và tiếp xúc với đường thẳng x + 2y + 3 = 0.

Lời giải:

a) Đường tròn có tâm I(– 2; 5) và bán kính R = 7 có phương trình là 

(x – (–2))² + (y – 5)² = 7² hay (x + 2)² + (y – 5)² = 49. 

b) Đường tròn có tâm I và đi qua điểm A nên bán kính đường tròn là IA. 

Ta có: IA = $\sqrt{{\left(-2-1\right)}^2+{\left(2-\left(-2\right)\right)}^2}$ = 5. 

Do đó phương trình đường tròn là: (x – 1)² + (y – (– 2))² = 5² 

Hay (x – 1)² + (y + 2)² = 25. 

c) Đường tròn có đường kính AB thì tâm của đường tròn này là trung điểm của AB.

Tọa độ trung điểm I của AB là I$\left(\frac{\left(-1\right)+\left(-3\right)}{2};\frac{\left(-3\right)+5}{2}\right)$ hay I(– 2; 1). 

Ta có: AB = $\sqrt{{\left(-3-\left(-1\right)\right)}^2+\left(5-{\left(-3\right)}^2\right)}$ = $2\sqrt{17}$. 

Khi đó phương trình đường tròn đường kính AB là: 

hay (x + 2)² + (y – 1)² = 68. 

d) Đường tròn (C) có tâm I(1; 3) và tiếp xúc với đường thẳng ∆: x + 2y + 3 = 0 thì khoảng cách từ tâm I đến ∆ chính bằng bán kính của (C). 

Ta có: R = d(I, ∆) = $\frac{\left|1+2.3+3\right|}{\sqrt{1^2+2^2}}=\frac{10}{\sqrt{5}}=2\sqrt{5}$. 

Vậy phương trình đường tròn (C) là: 

${\left(x-\left(-2\right)\right)}^2+{\left(y-1\right)}^2={\left(2\sqrt{17}\right)}^2$ hay (x – 1)² + (y – 3)² = 20. 

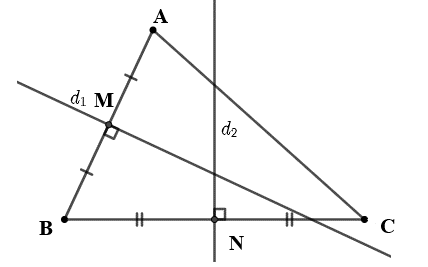
Bài 7.16 trang 47 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC, với A(6; – 2), B(4; 2), C(5; –5). Viết phương trình đường tròn ngoại tiếp tam giác đó. 

Lời giải:

Đường tròn ngoại tiếp tam giác ABC là đường tròn đi qua ba điểm A, B, C. 

Các đoạn thẳng AB, BC tương ứng có trung điểm là M(5; 0), N$\left(\frac{9}{2};\frac{-3}{2}\right)$. 

Đường thẳng trung trực d₁ của đoạn thẳng AB đi qua điểm M(5; 0) và có vectơ pháp tuyến $\overrightarrow{AB}=\left(-2;4\right)$. 

Vì $\overrightarrow{AB}=\left(-2;4\right)$ cùng phương với $\overrightarrow{n_1}=\left(1;-2\right)$ nên d₁ cũng nhận $\overrightarrow{n_1}=\left(1;-2\right)$ là vectơ pháp tuyến. Do đó, phương trình của d₁ là: 1(x – 5) – 2(y – 0) = 0 hay x – 2y – 5 = 0. 

Đường thẳng trung trực d₂ của đoạn thẳng BC đi qua N$\left(\frac{9}{2};\frac{-3}{2}\right)$ và có vectơ pháp tuyến $\overrightarrow{BC}=\left(1;-7\right)$ , do đó phương trình d₂ là:$1\left(x-\frac{9}{2}\right)-7\left(y+\frac{3}{2}\right)=0$ hay x – 7y – 15 = 0. 

Tâm I của đường tròn (C) ngoại tiếp tam giác ABC cách đều ba điểm A, B, C nên I là giao điểm của d₁ và d₂. 

Vậy tọa độ của I là nghiệm của hệ phương trình $\left\{\begin{array}{l}x-2y-5=0\\ x-7y-15=0\end{array}\right.$. 

Suy ra I(1; – 2). Đường tròn (C) có bán kính là IA = $\sqrt{{\left(6-1\right)}^2+{\left(-2-\left(-2\right)\right)}^2}=5$.

Vậy phương trình của (C) là: (x – 1)² + (y + 2)² = 25.

Bài 7.17 trang 47 Toán 10 Tập 2: Cho đường tròn (C): x² + y²+ 2x – 4y + 4  = 0. Viết phương trình tiếp tuyến d của (C) tại điểm M(0; 2).  

Lời giải:

Ta có: x² + y² + 2x – 4y + 4 = 0 ⇔ x² + y² – 2 . (– 1) . x – 2 . 2 . y + 4 = 0.

Các hệ số: a = – 1, b = 2, c = 4. 

Khi đó đường tròn (C) có tâm I(– 1; 2). 

Do 0² + 2² + 2 . 0 – 4 . 2 + 4 = 0 nên điểm M(0; 2) thuộc (C). 

Tiếp tuyến d của (C) tại điểm M(0; 2) có vectơ pháp tuyến $\overrightarrow{IM}=\left(0+1;2-2\right)=\left(1;0\right)$, nên có phương trình d: 1(x – 0) + 0(y – 2) = 0 hay d: x = 0. 

Bài 7.18 trang 47 Toán 10 Tập 2: Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ. Theo đó, tại thời điểm t (0 ≤ t ≤ 180) vật thể ở vị trí có tọa độ (2 + sint°; 4 + cost°). 

a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể. 

b) Tìm quỹ đạo chuyển động của vật thể. 

Lời giải:

a) Vị trí ban đầu của vật thể là tại thời điểm t = 0, nên tọa độ của điểm ở vị trí này là: 

(2 + sin0°; 4 + cos0°) = (2; 5).

Vị trí kết thúc của vật thể là tại thời điểm t = 180, nên tọa độ của điểm ở vị trí này là: 

(2 + sin 180°; 4 + cos 180°) = (2; 3).

b) Gọi điểm M(x; y) thuộc vào quỹ đạo chuyển động của vật thể.

Ta có: x = 2 + sin t°và y = 4 + cost°.

Suy ra: x – 2 = sin t° và y – 4 = cost°.

Mà sin² t° + cos² t° = 1     (0 ≤ t ≤ 180)

Do đó ta có: (x – 2)² + (y – 4)² = 1.

Vậy quỹ đạo chuyển động của vật thể là đường tròn có tâm I(2; 4) và bán kính R = 1.

Lời giải bài tập Toán lớp 10 Bài 21: Đường tròn trong mặt phẳng tọa độ Kết nối tri thức hay khác:

• Giải Toán 10 trang 43

• Giải Toán 10 trang 44

• Giải Toán 10 trang 45

• Giải Toán 10 trang 46