Bài 15 trang 58 Toán 11 Tập 1 Cánh diều
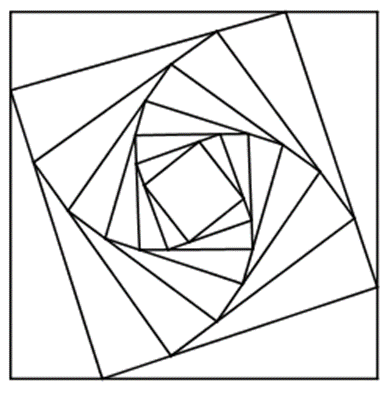
Cho hình vuông C có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C (Hình 4). Từ hình vuông C lại làm tiếp tục như trên để có hình vuông C. Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông C, C, C, ..., C, ... Gọi a là độ dài cạnh hình vuông C. Chứng minh dãy số (a) là cấp số nhân.
Giải Toán 11 Bài tập cuối chương 2 - Cánh diều
Bài 15 trang 58 Toán 11 Tập 1: Cho hình vuông C1 có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2 (Hình 4). Từ hình vuông C2 lại làm tiếp tục như trên để có hình vuông C3. Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông C1, C2, C3, ..., Cn, ... Gọi an là độ dài cạnh hình vuông Cn. Chứng minh dãy số (an) là cấp số nhân.
Lời giải:
Độ dài cạnh của hình vuông đầu tiên là: a1 = 4.
Độ dài cạnh của hình vuông thứ n là: an.
Độ dài cạnh của hình vuông thứ n + 1 là: an+1 = .
Suy ra:
Vậy (an) là một cấp số nhân với số hạng đầu a1 = 4 và công bội q = .
Lời giải bài tập Toán 11 Bài tập cuối chương 2 hay, chi tiết khác:
Bài 2 trang 57 Toán 11 Tập 1: Trong các dãy số sau, dãy số nào là cấp số cộng? ....
Bài 3 trang 57 Toán 11 Tập 1: Cho cấp số cộng (un) có số hạng đầu u1 = – 5, công sai d = 4 ....
Bài 4 trang 57 Toán 11 Tập 1: Tổng 100 số tự nhiên lẻ đầu tiên tính từ 1 là ....
Bài 6 trang 57 Toán 11 Tập 1: Cho cấp số nhân (un) có un = – 1, công bội q=- ....
Bài 7 trang 57 Toán 11 Tập 1: Trong các dãy số (un) sau đây, dãy số nào là dãy số tăng? ....