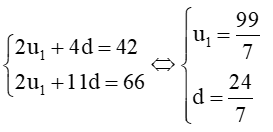Bài 9 trang 58 Toán 11 Tập 1 Cánh diều

Cho cấp số cộng (u). Tìm số hạng đầu u, công sai d trong mỗi trường hợp sau:

Giải Toán 11 Bài tập cuối chương 2 - Cánh diều

Bài 9 trang 58 Toán 11 Tập 1: Cho cấp số cộng (u_n). Tìm số hạng đầu u₁, công sai d trong mỗi trường hợp sau:

a) u₂ + u₅ = 42 và u₄ + u₉ = 66;

b) u₂ + u₄ = 22 và u₁.u₅ = 21.

Lời giải:

a) Ta có: u₂ + u₅ = u₁ + d + u₁ + 3d = 42

⇔ 2u₁ + 4d = 42

Ta lại có: u₄ + u₉ = u₁ + 3d + u₁ + 8d = 2u₁ + 11d = 66

Khi đó ta có hệ phương trình:

Bài 9 trang 58 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Vậy số hạng đầu của cấp số cộng là: $u_{1} = \frac{99}{7}$ và công sai d= $\frac{24}{7}$ .

b) Ta có: u₂ + u₄ = u₁ + d + u₁ + 3d = 22

⇔ 2u₁ + 4d = 22

⇔ u₁ + 2d = 11

⇔ u₁ = 11 – 2d

Ta lại có: u₁.u₅ = u₁(u₁ + 4d) = 21.

Thay u₁ = 11 – 2d vào biểu thức trên ra được:

(11 – 2d)(11 – 2d + 4d) = 21

⇔ (11 – 2d)(11 + 2d) = 21

⇔ 121 – 4d² = 21

⇔ d = 5 hoặc d = – 5.

Với d = 5 thì u₁ = 1.

Với d = – 5 thì u₁ = 21.

Lời giải bài tập Toán 11 Bài tập cuối chương 2 hay, chi tiết khác: