Bài 3 trang 104 Toán 11 Tập 1 Cánh diều
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI = 2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).
Giải Toán 11 Bài 3: Đường thẳng và mặt phẳng song song - Cánh diều
Bài 3 trang 104 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI = 2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).
Lời giải:
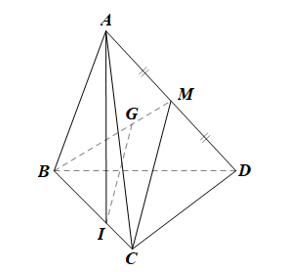
Gọi M là trung điểm của AD.
• Xét ABD có G là trọng tâm tam giác nên .
Theo bài, BI = 2IC nên
• Trong mặt phẳng (BCM):
Xét BCM có: , suy ra IG // CM (định lí Thalès đảo)
• Ta có: IG // CM; CM ⊂ (ACD)
Do đó IG // (ACD).
Lời giải bài tập Toán 11 Bài 3: Đường thẳng và mặt phẳng song song hay, chi tiết khác:
Câu hỏi khởi động trang 101 Toán 11 Tập 1: Trong thực tiễn, ta thường gặp nhiều đồ dùng, vật thể gợi nên hình ảnh đường thẳng song song với mặt phẳng....
Hoạt động 1 trang 101 Toán 11 Tập 1: a) Trong Hình 44, thanh barrier và mặt phẳng gợi nên hình ảnh đường thẳng d và mặt phẳng (P). Cho biết đường thẳng d và mặt phẳng (P) có điểm chung hay không. ....
Luyện tập 1 trang 102 Toán 11 Tập 1: Quan sát các xà ngang trên sân tập thể dục Hình 47. Hãy cho biết ở vị trí tương đối của các xà ngang đó đối với mặt sàn. ....
Hoạt động 2 trang 102 Toán 11 Tập 1: Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48)....
Luyện tập 2 trang 102 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao? ....
Hoạt động 3 trang 102, 103 Toán 11 Tập 1: Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b. (Hình 51). ...
Luyện tập 3 trang 103 Toán 11 Tập 1: Ở Ví dụ 3, xác định giao tuyến của mặt phẳng (R) với các mặt phẳng (ABD), (BCD), (ACD). ....
Hoạt động 4 trang 103 Toán 11 Tập 1: Cho hai mặt phẳng (P), (Q) cùng song song với đường thẳng a và (P) ∩ (Q) = b (Hình 54). ....

