Hoạt động 2 trang 102 Toán 11 Tập 1 Cánh diều
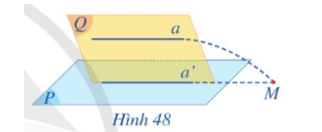
Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48). Gọi (Q) là mặt phẳng xác định bởi hai đường thẳng song song a, a’.
Giải Toán 11 Bài 3: Đường thẳng và mặt phẳng song song - Cánh diều
Hoạt động 2 trang 102 Toán 11 Tập 1: Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48). Gọi (Q) là mặt phẳng xác định bởi hai đường thẳng song song a, a’.
a) Giả sử a cắt (P) tại M. Đường thẳng a có cắt đường thẳng a’ tại M hay không?
b) Nêu vị trí tương đối của đường thẳng a và mặt phẳng (P). Vì sao?
Lời giải:
a) Do a’ ⊂ (P) và a’ ⊂ (Q) nên (P) ∩ (Q) = a’.
Mà a cắt (P) tại M nên M ∈ (P)
Lại có M ∈ a, a ⊂ (Q) nên M ∈ (Q)
Suy ra M là giao điểm của (P) và (Q).
Do đó giao tuyến a’ của hai mặt phẳng đi qua điểm M.
Vậy đường thẳng a cắt đường thẳng a’ tại M.
b) Theo câu a, nếu a cắt (P) tại M thì đường thẳng a và đường thẳng a’ cắt nhau tại M.
Điều này là mâu thuẫn với giả thiết là hai đường thẳng a và a’ song song.
Do đó a không có điểm chung với (P) nên a // (P).
Lời giải bài tập Toán 11 Bài 3: Đường thẳng và mặt phẳng song song hay, chi tiết khác: