Giải Toán 11 trang 62 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm lời giải Toán 11 trang 62 Tập 2 trong Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm Toán 11 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 62.

Giải Toán 11 trang 62 Tập 2 Cánh diều

Luyện tập 2 trang 62 Toán 11 Tập 2: Tính đạo hàm của hàm số f(x) = x³ tại điểm x bất kì bằng định nghĩa.

Lời giải:

⦁ Xét ∆x là số gia của biến số tại điểm x.

Ta có ∆y = f(x + ∆x) – f(x) = (x + ∆x)³ – x³

              = x³ + 3x²∆x + 3x(∆x)² + (∆x)³ – x³

              = 3x²∆x + 3x(∆x)² + (∆x)³

              = ∆x[3x² + 3x∆x + (∆x)²]

Suy ra $\frac{\Delta y}{\Delta x}=\frac{\Delta x\left[3x^2+3x\Delta x+{\left(\Delta x\right)}^2\right]}{\Delta x}=3x^2+3x\Delta x+{\left(\Delta x\right)}^2.$

⦁ Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\left[3x^2+3x\cdot \Delta x+{\left(\Delta x\right)}^2\right]=3x^2+3\Delta x\cdot 0+0^2=3x^2.$

Vậy f’(x) = 3x².

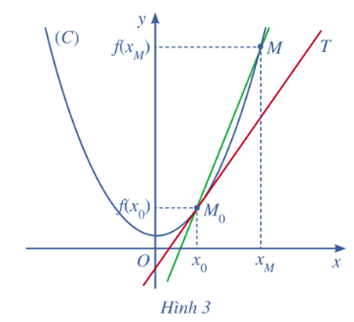
Hoạt động 2 trang 62 Toán 11 Tập 2: Cho hàm số y = f(x) có đồ thị (C), một điểm M₀ cố định thuộc (C) có hoành độ x₀. Với mỗi điểm M thuộc (C) khác M₀, kí hiệu x_M là hoành độ của điểm M và k_M là hệ số góc của cát tuyến M₀M. Giả sử tồn tại giới hạn hữu hạn$k_0=\underset{x_M\to x_0}{\lim }{k}_M$ .

Khi đó, ta coi đường thẳng M₀T đi qua M₀ và có hệ số góc k₀ là vị trí giới hạn của cát tuyến M₀M khi điểm M di chuyển dọc theo (C) dần tới M₀.

Đường thẳng M₀T được gọi là tiếp tuyến của (C) tại điểm M₀, còn M₀ được gọi là tiếp điểm (Hình 3).

a) Xác định hệ số góc k₀ của tiếp tuyến M₀T theo x₀.

b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M₀

Lời giải:

a)Từ M₀(x₀; y₀) và M(x_M; y_M) ta có $\overrightarrow{M_{0}M}=\left(x_M-x_0;y_M-y_0\right)$

Đường cát tuyến $\overrightarrow{M_{0}M}=\left(x_M-x_0;y_M-y_0\right)$ nhận làm vectơ chỉ phương nên có

Hệ số góc là: $k_M=\frac{y_M-y_0}{x_M-x_0}=\frac{f\left(x_M\right)-f\left(x_0\right)}{x_M-x_0}$

Khi đó: $k_0=\underset{x_M\to x_0}{\lim }{k}_M=\underset{x_M\to x_0}{\lim }\frac{f\left(x_M\right)-f\left(x_0\right)}{x_M-x_0}=f^{\text{'}}\left(x_0\right).$

Vậy k₀ = f’(x₀).

b) Phương trình tiếp tuyến của đồ thị hàm số tại điểm M₀(x₀; y₀) có hệ số góc k₀ = f’(x₀)là:

y = k₀(x – x₀) + y₀ hay y = f’(x₀)(x – x₀) + f(x₀).

Lời giải bài tập Toán 11 Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm hay khác:

• Giải Toán 11 trang 63