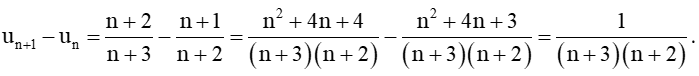Bài 3 trang 61 Toán 11 Tập 1 Chân trời sáng tạo

Cho dãy số (u) với . Phát biểu nào sau đây là đúng?

Giải Toán 11 Bài tập cuối chương 2 - Chân trời sáng tạo

Bài 3 trang 61 Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{n + 1}{n + 2}$ . Phát biểu nào sau đây là đúng?

A. Dãy số tăng và bị chặn;

B. Dãy số giảm và bị chặn;

C. Dãy số giảm và bị chặn dưới;

D. Dãy số giảm và bị chặn trên.

Lời giải:

Đáp án đúng là: A

+) Ta có: $u_{n + 1} = \frac{n + 1 + 1}{n + 1 + 2} = \frac{n + 2}{n + 3}$

Xét hiệu Bài 3 trang 61 Toán 11 Tập 1 Chân trời sáng tạo

Vì n ∈ ℕ^* nên n > 0, suy ra $\frac{1}{(n + 3) (n + 2)} > 0$ .

Do đó u_n+1 > u_n hay (u_n) là dãy tăng.

+) Ta có: $u_{n} = 1 - \frac{1}{n + 2}$

Vì n ∈ ℕ^* nên n ≥ 1 suy ra n + 2 ≥ 3

$\Rightarrow u_{n} = 1 - \frac{1}{n + 2} \geq 1 - \frac{1}{3} = \frac{2}{3}, \forall n \in ℕ^{*}$ .

Ta lại có n ∈ ℕ^* nên n > 0 suy ra $\frac{1}{n + 2} > 0$ . Do đó $u_{n} = 1 - \frac{1}{n + 2} < 1$ .

Vì vậy $\frac{2}{3} \leq u_{n} < 1$ nên dãy số (u_n) bị chặn.

Lời giải bài tập Toán 11 Bài tập cuối chương 2 hay, chi tiết khác: