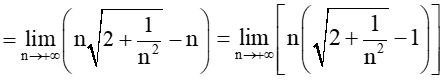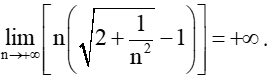Bài 5.3 trang 109 Toán 11 Tập 1 - Kết nối tri thức

Tìm giới hạn của các dãy số cho bởi:

Giải Toán 11 Bài 15: Giới hạn của dãy số - Kết nối tri thức

Bài 5.3 trang 109 Toán 11 Tập 1: Tìm giới hạn của các dãy số cho bởi:

a) $u_n=\frac{n^2+1}{2n-1}$;

b) $v_n=\sqrt{2n^2+1}-n$.

Lời giải:

a) $u_n=\frac{n^2+1}{2n-1}$

Chia cả tử và mẫu của u_n cho n², ta được $u_n=\frac{n^2+1}{2n-1}$$=\frac{1+\frac{1}{n^2}}{\frac{2}{n}-\frac{1}{n^2}}$.

Vì $\underset{n\to +\infty }{\lim }\left(1+\frac{1}{n^2}\right)=1>0$, $\underset{n\to +\infty }{\lim }\left(\frac{2}{n}-\frac{1}{n^2}\right)=0$ và $\frac{2}{n}-\frac{1}{n^2}>0$ với mọi n nên

$\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }\frac{n^2+1}{2n-1}=+\infty$.

b) $v_n=\sqrt{2n^2+1}-n$

Ta có: $\underset{n\to +\infty }{\lim }{v}_n=\underset{n\to +\infty }{\lim }\left(\sqrt{2n^2+1}-n\right)$$=\underset{n\to +\infty }{\lim }\left(\sqrt{n^2\left(2+\frac{1}{n^2}\right)}-n\right)$

Vì $\underset{n\to +\infty }{\lim }\left(\sqrt{2+\frac{1}{n^2}}-1\right)=\sqrt{2}-1>0$ và $\underset{n\to +\infty }{\lim }n=+\infty$.

Nên

Vậy $\underset{n\to +\infty }{\lim }{v}_n=\underset{n\to +\infty }{\lim }\left(\sqrt{2n^2+1}-n\right)=+\infty$.

Lời giải bài tập Toán 11 Bài 15: Giới hạn của dãy số hay, chi tiết khác:

• HĐ1 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn là 0 ....

• Luyện tập 1 trang 105 Toán 11 Tập 1: Chứng minh rằng $\underset{n\to +\infty }{\lim }\frac{{\left(-1\right)}^{n-1}}{3^n}=0$ ....

• HĐ2 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn hữu hạn ....

• Luyện tập 2 trang 106 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{{3.2}^n-1}{2^n}$ . Chứng minh rằng $\underset{n\to +\infty }{\lim }{u}_n=3$ ....

• Vận dụng 1 trang 106 Toán 11 Tập 1: Một quả bóng cao su được thả từ độ cao 5 m xuống mặt sàn ....

• HĐ3 trang 106 Toán 11 Tập 1: Hình thành quy tắc tính giới hạn Cho hai dãy số (un) và (vn)....

• Luyện tập 3 trang 107 Toán 11 Tập 1: Tìm $\underset{n\to +\infty }{\lim }\frac{\sqrt{2n^2+1}}{n+1}$ ....

• HĐ4 trang 107 Toán 11 Tập 1: Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau ....

• Luyện tập 4 trang 108 Toán 11 Tập 1: Tính tổng $S=2+\frac{2}{7}+\frac{2}{49}+\mathrm{...}+\frac{2}{7^{n-1}}+\mathrm{...}$ ....

• Vận dụng 2 trang 108 Toán 11 Tập 1: Để đơn giản, ta giả sử Achilles chạy với vận tốc 100 km/h, vận tốc của rùa là 1 km/h ....

• HĐ5 trang 108 Toán 11 Tập 1: Một loại vi khuẩn được nuôi cấy với số lượng ban đầu là 50. Sau mỗi chu kì 4 giờ, số lượng của chúng sẽ tăng gấp đôi ....

• Luyện tập 5 trang 109 Toán 11 Tập 1: Tính $\underset{n\to +\infty }{\lim }\left(n-\sqrt{n}\right)$. ....

• Bài 5.1 trang 109 Toán 11 Tập 1: Tìm các giới hạn sau: ....

• Bài 5.2 trang 109 Toán 11 Tập 1: Cho hai dãy số không âm (un) và (vn) ....

• Bài 5.4 trang 109 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số ....

• Bài 5.5 trang 109 Toán 11 Tập 1: Một bệnh nhân hằng ngày phải uống một viên thuốc 150 mg ....

• Bài 5.6 trang 109 Toán 11 Tập 1: Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3) ....