Bài 5.6 trang 109 Toán 11 Tập 1 - Kết nối tri thức
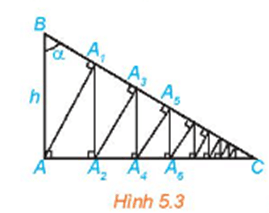
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA ⊥ BC, từ A kẻ AA ⊥ AC, sau đó lại kẻ AA ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AAAA... Tính độ dài đường gấp khúc này theo h và α.
Giải Toán 11 Bài 15: Giới hạn của dãy số - Kết nối tri thức
Bài 5.6 trang 109 Toán 11 Tập 1: Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA1 ⊥ BC, từ A1 kẻ A1A2 ⊥ AC, sau đó lại kẻ A2A3 ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA1A2A3... Tính độ dài đường gấp khúc này theo h và α.
Lời giải:
Tam giác AA1B vuông tại A1 có AB = h và .
Do đó, AA1 = AB sinB = h sin α.
Ta có: và , suy ra .
Tam giác AA1A2 vuông tại A2 nên A1A2 = AA1 sin = h sin α . sin α = h sin2 α.
Vì AB ⊥ AC và A1A2 ⊥ AC nên AB // A1A2, suy ra (2 góc đồng vị).
Tam giác A1A2A3 vuông tại A3 nên A2A3 = A1A2 . sin = h sin2 α . sin α = h sin3 α.
Vì AA1 ⊥ BC và A2A3 ⊥ BC nên AA1 // A2A3, suy ra .
Tam giác A2A3A4 vuông tại A4 nên A3A4 = A2A3 . sin = h sin3 α . sin α = h sin4 α.
Cứ tiếp tục như vậy, ta xác định được An – 1An = h sinn α.
Ta có: AA1A2A3... = AA1 + A1A2 + A2A3 + ... + An – 1An + ...
= h sin α + h sin2 α + h sin3 α + ... + h sinn α + ...
Vì góc B là góc nhọn nên sin B = sin α < 1, do đó |sin α| < 1.
Khi đó, độ dài của đường gấp khúc vô hạn AA1A2A3... là tổng của cấp số nhân lùi vô hạn với số hạng đầu u1 = h sin α và công bội q = sin α.
Do đó, AA1A2A3... = .
Lời giải bài tập Toán 11 Bài 15: Giới hạn của dãy số hay, chi tiết khác:
HĐ1 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn là 0 ....
HĐ2 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn hữu hạn ....
Luyện tập 2 trang 106 Toán 11 Tập 1: Cho dãy số (un) với . Chứng minh rằng ....
Vận dụng 1 trang 106 Toán 11 Tập 1: Một quả bóng cao su được thả từ độ cao 5 m xuống mặt sàn ....
HĐ3 trang 106 Toán 11 Tập 1: Hình thành quy tắc tính giới hạn Cho hai dãy số (un) và (vn)....