Cho hai dãy số không âm (un) và (vn) với lim n đến + vô cùng un = 2 và lim n đến + vô cùng vn = 3. Tìm các giới hạn sau: a) lim n đến + vô cùng un^2/vn - un;
Câu hỏi:
Cho hai dãy số không âm (un) và (vn) với \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\) và \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = 3\). Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{u_n^2}}{{{v_n} - {u_n}}}\);
b) \(\mathop {\lim }\limits_{n \to + \infty } \sqrt {{u_n} + 2{v_n}} \).
Trả lời:
Lời giải:
a) Ta có: \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\), do đó, \(\mathop {\lim }\limits_{n \to + \infty } u_n^2 = \mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}.{u_n}} \right) = 2.2 = 4\).
Và \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = 3\) nên \(\mathop {\lim }\limits_{n \to + \infty } \left( {{v_n} - {u_n}} \right) = 3 - 2 = 1\).
Vậy \(\mathop {\lim }\limits_{n \to + \infty } \frac{{u_n^2}}{{{v_n} - {u_n}}} = \frac{4}{1} = 4\).
b) Ta có: \(\mathop {\lim }\limits_{n \to + \infty } 2 = 2\) và \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = 3\), do đó, \(\mathop {\lim }\limits_{n \to + \infty } \left( {2{v_n}} \right) = \mathop {\lim }\limits_{n \to + \infty } \left( {2.{v_n}} \right) = 2.3 = 6\).
Và \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\) nên \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + 2{v_n}} \right) = 2 + 6 = 8\).
Vì un ≥ 0, vn ≥ 0 với mọi n nên un + 2vn ≥ 0 với mọi n và \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + 2{v_n}} \right) = 8 > 0\).
Do đó, \(\mathop {\lim }\limits_{n \to + \infty } \sqrt {{u_n} + 2{v_n}} = \sqrt 8 = 2\sqrt 2 \).
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Cho dãy số (un) với \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\).
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ un đến 0 nhỏ hơn 0,01?
Xem lời giải »
Câu 2:
Chứng minh rằng \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}} = 0\).
Xem lời giải »
Câu 3:
Cho dãy số (un) với \({u_n} = \frac{{n + {{\left( { - 1} \right)}^n}}}{n}\). Xét dãy số (vn) xác định bởi vn = un – 1.
Tính \(\mathop {\lim }\limits_{n \to + \infty } {v_n}\).
Xem lời giải »
Câu 4:
Cho dãy số (un) với \({u_n} = \frac{{{{3.2}^n} - 1}}{{{2^n}}}\). Chứng minh rằng \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 3\).
Xem lời giải »
Câu 5:
Tìm giới hạn của các dãy số cho bởi:
a) \({u_n} = \frac{{{n^2} + 1}}{{2n - 1}}\);
b) \({v_n} = \sqrt {2{n^2} + 1} - n\).
Xem lời giải »
Câu 6:
Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số:
a) 1,(12) = 1,121212...;
b) 3,(102) = 3,102102102...
Xem lời giải »
Câu 7:
Một bệnh nhân hằng ngày phải uống một viên thuốc 150 mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể bệnh nhân nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
Xem lời giải »
Câu 8:
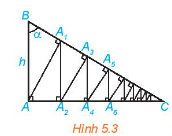
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA1 ⊥ BC, từ A1 kẻ A1A2 ⊥ AC, sau đó lại kẻ A2A3 ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA1A2A3... Tính độ dài đường gấp khúc này theo h và α.
Xem lời giải »