Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng: a) MN là đường vuông góc chung của AB và CD.
Câu hỏi:
Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
Trả lời:
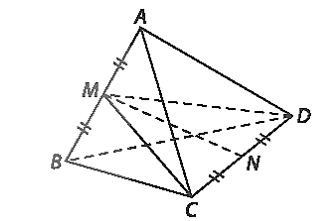
a) Xét tam giác ADB có AD = BD = a nên tam giác ADB cân tại D.
Vì M là trung điểm của AB nên DM là trung tuyến.
Vì tam giác ADB cân tại D, DM là trung tuyến nên DM đồng thời là đường cao hay DM ^ AB.
Xét tam giác ABC có AC = BC = a nên tam giác ABC cân tại C mà CM là trung tuyến nên CM là đường cao hay CM ^ AB.
Vì DM ^ AB và CM ^ AB nên AB ^ (DCM), suy ra AB ^ MN.
Xét tam giác ADC có AD = AC = a nên tam giác ACD cân tại A mà AN là trung tuyến nên AN đồng thời là đường cao hay AN ^ CD.
Xét tam giác BCD có BD = BC = a nên tam giác BCD cân tại B mà BN là trung tuyến nên BN đồng thời là đường cao hay BN ^ CD.
Vì AN ^ CD và BN ^ CD nên CD ^ (ABN), suy ra CD ^ MN.
Vì AB ^ MN và CD ^ MN nên MN là đường vuông góc chung của AB và CD.