HĐ7 trang 29 Toán 11 Tập 1 - Kết nối tri thức

Cho hàm số y = cot x.

Giải Toán 11 Bài 3: Hàm số lượng giác - Kết nối tri thức

HĐ7 trang 29 Toán 11 Tập 1: Cho hàm số y = cot x.

a) Xét tính chẵn, lẻ của hàm số.

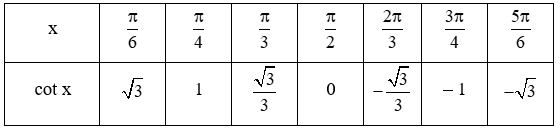
b) Hoàn thành bảng giá trị sau của hàm số y = cot x trên khoảng (0; π).

HĐ7 trang 29 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11

Bằng cách lấy nhiều điểm M(x; cot x) với x ∈ (0; π) và nối lại ta được đồ thị hàm số y = cot x trên khoảng (0; π).

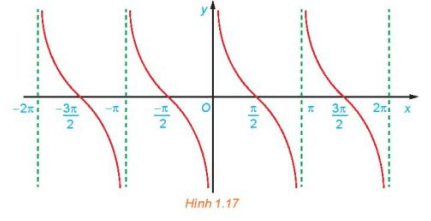
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = cot x như hình dưới đây.

HĐ7 trang 29 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11

Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số y = cotx.

Lời giải:

a) Hàm số y = f(x) = cot x có tập xác định là D = ℝ \ {kπ | k ∈ ℤ}.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = cot (– x) = – cot x = – f(x), ∀ x ∈ D.

Vậy y = cot x là hàm số lẻ.

b) Ta có: $\cot \frac{π}{6} = \sqrt{3}, \cot \frac{π}{4} = 1, \cot \frac{π}{3} = \frac{\sqrt{3}}{3}, \cot \frac{π}{2} = 0$ ,

$\cot \frac{2 π}{3} = - \frac{\sqrt{3}}{3}, \cot \frac{3 π}{4} = - 1, \cot \frac{5 π}{6} = - \sqrt{3}$ .

Vậy ta hoàn thành được bảng như sau:

HĐ7 trang 29 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11

c) Quan sát Hình 1.17, ta thấy đồ thị hàm số y = cot x có:

+) Tập giá trị là ℝ;

+) Nghịch biến trên mỗi khoảng $(k π; π + k π), k \in ℤ$ (do đồ thị hàm số đi xuống từ trái sang phải trên mỗi khoảng này).

Lời giải bài tập Toán 11 Bài 3: Hàm số lượng giác hay, chi tiết khác: